|
Just incase any document encrypted, use this password 'siri2u!'
FORM 1
FORM 2
FORM 3
FORM 4
PHYSICS SYLLABUS TOPICS
2 Comments
MEASUREMENT I
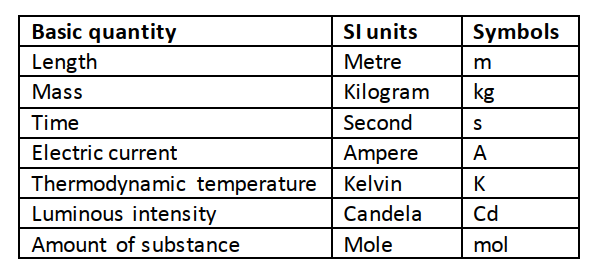
In order to measure we need to know or define the quantity to be measured and the units for measuring it. In 1971 a system known as the International System of Units (Systeme’ Internationale) and seven basic units were agreed upon as follows.
Other quantities can be obtained from these basic quantities and are referred to as derived quantities. LengthThis is the measure of distance between two points in space. The SI unit for length is the metre (m).Therefore 1 km = 1000 m
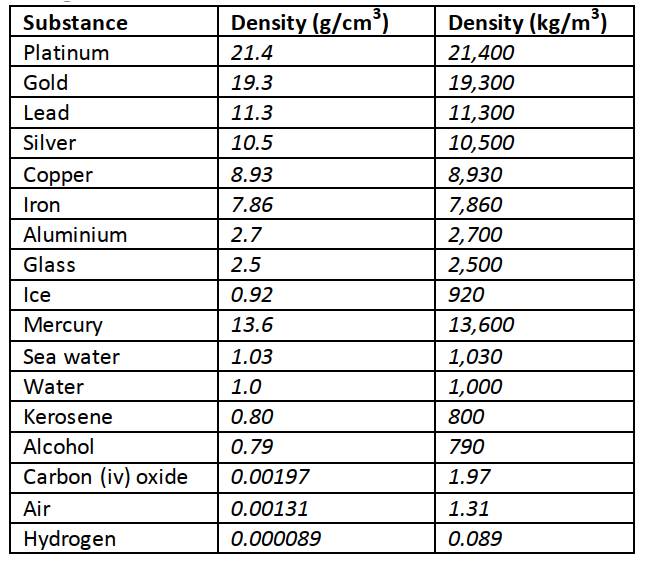
1 Hm = 100 m Length is measured using a metre rule (100 cm), tape measure (100 m, 300 m, 500 m)1 Dm= 10 m 1 mm = 0.001 m AreaThis is the measure of the extent of a surface. It is a derived quantity of length. Its SI units are square metres (m2). Other units are cm2, km2, etc. Formulas are used to determine areas of regular bodies while for irregular bodies an approximation of area is used.VolumeThis is the amount of space occupied by matter. The SI units for volume is cubic metre (m3). Other sub-multiples are cm3, mm3 and l. Hence 1 m3 = 1,000,000 cm3 and 1litre = 1,000 cm3. Volume can be measured using a measuring cylinder, eureka can, pipette, burette, volumetric flask, beaker, etc.MassThis is the quantity of matter contained in a substance. Matter is anything that occupies space and has weight. The SI unit for mass is the Kilogram (kg). Other sub-multiples used are grams (g), milligrams (mg) and tonnes (t). 1 kg = 1,000 g = 1,000,000 mg=100 tonnes. A beam balance is used to measure mass.DensityThis is mass per unit volume of a substance. It is symbolized by rho (ρ) and its SI units are kg/m3. Density = mass / volume.Examples
Example
The mass of an empty density bottle is 20 g. Its mass when filled with water is 40.0 g and 50.0 g when filled with liquid X. Calculate the density of liquid X if the density of water is 1,000 kgm-3. Solution
Mass of water = 40 – 20 = 20 g = 0.02 kg. Volume of water = 0.02 / 1,000 = 0.00002 m3. Volume of liquid = volume of bottle Mass of liquid = 50 – 20 = 30 g = 0.03 kg Therefore density of liquid = 0.03 / 0.00002 = 1,500 kgm-3 Relative densityThis is the density of a substance compared to the density of water.It is symbolized by (d) and has no units since it’s a ratio. Relative density (d) = density of substance / density of water. It is measured using a relative density bottle ExampleThe relative density of some type of wood is 0.8. Find the density of the wood in kg/m3.Solution
Density of substance = d × density of water
Density of substance = 0.8 × 1,000 = 800 kgm-3 Densities of mixtures
We use the following formula to calculate densities of mixtures Density of the mixture = mass of the mixture / volume of the mixture Example100 cm3 of fresh water of density 1,000 kgm-3 is mixed with 100 cm3 of sea water of density 1030 kgm-3. Calculate the density of the mixture.Solution
Mass = density × volume Mass of fresh water = 1,000 × 0.0001 = 0.1 kg Mass of sea water = 1030 × 0.0001 = 0.103 kg Mass of mixture = 0.1 + 0.103 = 0.203 kg Volume of mixture = 100 + 100 = 200 cm3 = 0.0002 m3 Therefore density = mass / volume = 0.203 / 0.0002 =1,015 kg/m3. TimeThis is a measure of duration of an event. The SI unit for time is the second (s). Submultiples of the second are milliseconds, microseconds, minute, hour, day, week and year. It is measured using clocks, stop watches, wrist watches, and digital watches.Accuracy and errorsAccuracy is the closeness of a measurement to the correct value of the quantity being measured. It is expressed as an error. An error is therefore the deviation of measurement to the correct value being measured. The smaller the error the accurate the measurement.% error = (sensitivity / size measured) × 100. MEASUREMENTS 1 - KCSE PHYSICS NOTES, AUDIOVISUALS, OBJECTIVES, QUESTIONS, SCHEMES OF WORK AND ANSWERS
<
>
SPECIFIC OBJECTIVES
By the end of the course, the learner should be able to:
TOPICS / SUB-TOPICS OUTLINE:
MEASUREMENTS 1
In order to measure we need to know or define the quantity to be measured and the units for measuring it. In 1971 a system known as the International System of Units (Systeme’ Internationale) and seven basic units were agreed upon as follows. Other quantities can be obtained from these basic quantities and are referred to as derived quantities.
Length
This is the measure of distance between two points in space. The SI unit for length is the metre (m). Therefore;
Area
This is the measure of the extent of a surface. It is a derived quantity of length. Its SI units are square metres (m2). Other units are cm2, km2 etc. Formulas are used to determine areas of regular bodies while for irregular bodies an approximation of area is used.
Volume
This is the amount of space occupied by matter. The SI units for volume is cubic metre (m3). Other sub-multiples are cm3, mm3 and l. Hence 1 m3 = 1,000,000 cm3 and 1l= 1,000 cm3. Volume can be measured using a measuring cylinder, eureka can, pipette, burette, volumetric flask, beaker, etc.
Mass
This is the quantity of matter contained in a substance. Matter is anything that occupies space and has weight. The SI unit for mass is the Kilogram (kg). Other sub-multiples used are grams (g), milligrams (mg) and tonnes (t). 1 kg = 1,000 g = 1,000,000 mg=100 tonnes. A beam balance is used to measure mass.
MEASUREMENT 1 QUESTIONS
TOPICAL QUESTIONSSCHEMES OF WORK |
Archives
December 2024
Categories
All
Physics notes form 1 to 4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Primary Resources
College Resources
|
Secondary Resources
|
Contact Us
Manyam Franchise
P.O Box 1189 - 40200 Kisii Tel: 0728 450 424 Tel: 0738 619 279 E-mail - sales@manyamfranchise.com |
 RSS Feed
RSS Feed

