Transforming Math Education: From Memorization to Critical Thinking
Why do many people find math challenging?
​As a mathematics PhD student who has tutored and taught math extensively, I've observed a common issue among my classmates and students: they perceive math as a matter of memorizing formulas and applying them. Unfortunately, this instructional approach is often ineffective. To illustrate the difference, let me provide an example comparing two teaching methods for a simple concept: ​Method 1:
​The teacher presents a list of area formulas for various shapes, such as equilateral triangles, squares, rectangles, right triangles, and regular hexagons. These shapes may appear quite distinct, each with its own formula.
​Method 2:
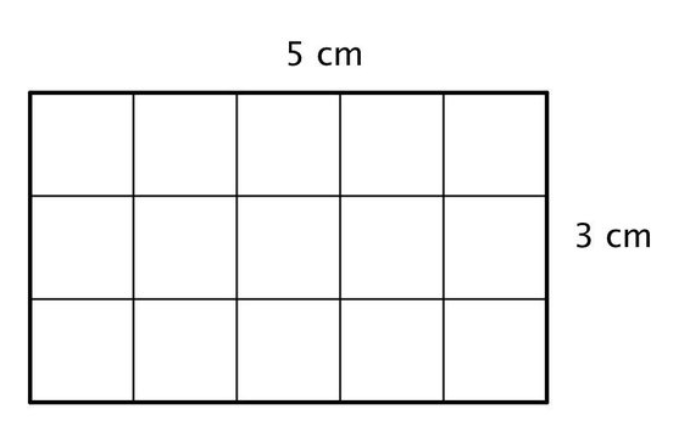
​The teacher visually demonstrates why the area of a rectangle equals its width multiplied by its height, using a diagram.
By counting the squares within the rectangle, students can clearly see that the area is 15. By exploring further examples, students will realize that multiplying the side lengths yields the area.
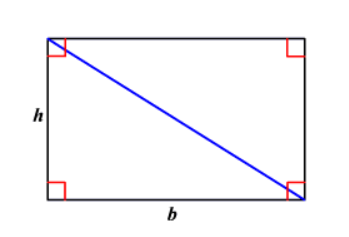
​ Building on this understanding, the teacher guides students to derive the formula for the area of a square based on the rectangle area formula, as squares are a special type of rectangle. At this point, students can deduce the area formula for right triangles by observing that two identical right triangles form a rectangle. Consequently, the area of the triangle is half the area of the rectangle, expressed as (1/2)base*height. 
Next, the teacher introduces the formula for the area of an equilateral triangle (a triangle with all sides of equal length), which is x^2 * (√3/4), where x represents the side length.
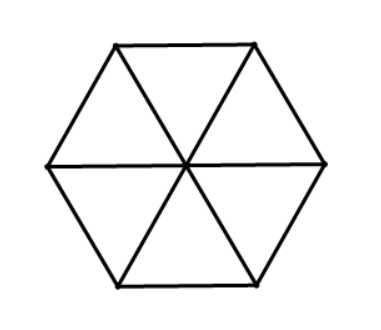
​ Using this knowledge, students can construct the area formula for regular hexagons (six-sided shapes with equal side lengths and angles) by envisioning a regular hexagon as six equilateral triangles combined (each with side length x). ​Thus, the area of a regular hexagon becomes six times the area of each equilateral triangle, which can be simplified to 3x^2 * (√2/3). 
The key distinction between these teaching methods lies in the fact that the first method requires memorizing five seemingly unrelated equations. If students forget any of these formulas, they will struggle with related problems, leading to frustration. This isolated and uninteresting approach often leads students to lose interest in math.
In contrast, the second method cultivates critical thinking rather than rote memorization. In this approach, students only need to remember one formula. They can recreate any other formula during tests or while working on homework. Furthermore, they will be able to derive formulas for other shapes, such as octagons or parallelograms. Students taught in this manner develop connections between seemingly disparate branches of math and appreciate the captivating intricacies within the subject.
Naturally, it also helps when teachers relate math to real-world applications. Merely learning area formulas for different shapes may seem pointless to some students. However, if teachers explain the practical significance of these formulas, the concepts are more likely to resonate. For example, students can explore the perimeters (side lengths) of shapes with the same area, contemplating questions like: If a square and a circle have the same area, what are their respective perimeters? Teachers can then illustrate how this concept appears in nature, such as the formation of spherical bubbles, which minimize surface area (analogous to perimeter) relative to volume (analogous to area). To demonstrate this, teachers can bring in bubbles and various tools folded into different shapes, showing that regardless of the shape of the bubble wand, the resulting bubbles always assume a spherical form. ​
This connection reinforces students' understanding, as they witness how circles (two-dimensional versions of spheres) also minimize perimeters.
Note: It's worth mentioning that this teaching method can be applied to non-visual problems as well. The focus is not solely on visual aids (although visualizing math is beneficial) but rather on explaining the process of obtaining formulas. This approach can be employed even for highly algebraic problems.
CITATION:BY Samantha Moore FIRST APPEARED ON QUORA
​People also like seeing why tricks work after seeing a trick work, in my experience. This happened when in the course of conversation, someone mentioned 51*49 as what they needed but didn't have a calculator handy. I said I didn't need a calculator, it's 2499. Astonished, he asked how I could multiply so fast.
Rather than tell him that it just happened to be two numbers that I had used consistently in algebra tutoring, I gave him the lesson. (x+1)*(x-1)=x^2-1 It's basic algebra, but now given form. I said because I know this, I can derive that two numbers multiplied together that are exactly two apart are always going to be easy. I find the square of the number in between and subtract one. After he found a calculator, he tried it on a few other numbers. Finding it to be true, and thoroughly impressed, he asked if there were any other secrets I was keeping from him. If people never find an application for math that they deem worthwhile or, at the very least, interesting, they tend to not care about the really neat and interesting applications that are available out in the world.
0 Comments
The Concept of the Messiah in the New TestamentThe concept of the Messiah in the New Testament is a central theme in Christian theology. It refers to Jesus Christ as the fulfillment of Old Testament prophecies and the savior of humanity. The New Testament portrays Jesus as the anointed one, the Son of God, who came to Earth to bring salvation and reconcile humanity with God. Key aspects of the concept of the Messiah in the New Testament include:
Learn more:X^3+x^2-x-1thus determine the stationary points and their nature
Explore the analysis of stationary points in the cubic function f(x) = x^3 + x^2 - x - 1. Learn how to find and interpret these points, including their nature as maximum or minimum points. Gain insights into the derivative and second derivative to determine the behavior of the function around these critical points.
To determine the stationary points and their nature for the function f(x) = x^3 + x^2 - x - 1, we need to find the derivative and solve for values of x where the derivative equals zero.
First, let's find the derivative of f(x): f'(x) = 3x^2 + 2x - 1 Next, we equate the derivative to zero and solve for x: 3x^2 + 2x - 1 = 0 This equation can be solved using various methods, such as factoring, completing the square, or using the quadratic formula. Let's use the quadratic formula in this case: x = (-b ± √(b^2 - 4ac)) / (2a) For our equation, a = 3, b = 2, and c = -1. Plugging in these values: x = (-2 ± √(2^2 - 43(-1))) / (2*3) x = (-2 ± √(4 + 12)) / 6 x = (-2 ± √16) / 6 x = (-2 ± 4) / 6 This gives us two possible values for x: x1 = (-2 + 4) / 6 = 2/6 = 1/3 x2 = (-2 - 4) / 6 = -6/6 = -1 Now, we have two potential stationary points: (1/3, f(1/3)) and (-1, f(-1)). To determine their nature (whether they are maximum, minimum, or inflection points), we can analyze the second derivative or observe the behavior of the function around these points. Taking the second derivative of f(x): f''(x) = 6x + 2 Substituting x = 1/3: f''(1/3) = 6(1/3) + 2 = 2 + 2 = 4 Since the second derivative is positive, f(1/3) is a minimum point. For x = -1: f''(-1) = 6(-1) + 2 = -6 + 2 = -4 Since the second derivative is negative, f(-1) is a maximum point. Therefore, the nature of the stationary points is as follows:
TWO TYPES OF DEVELOPMENT BY AFRICAN SOCIETY
Factors Influencing Mineral OccurrenceFactors influencing the occurrence of minerals can be attributed to various physical and chemical conditions. These factors play a crucial role in determining where and how minerals are formed. Here are some key factors that influence the occurrence of minerals:
Learn more: |
Archives
October 2023
Categories
All
ATIKA SCHOOL TEAMWe offer solutions to emerging problems |
RSS Feed