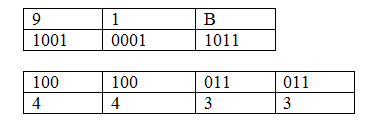
Work out the hexadecimal equivalent of 1011111000112Work out the hexadecimal equivalent of 1011111000112Divide in to 4 bits1011/1110/0011 Work out the hexadecimal of each group 1011-ll thus B 1110 = 14 thus E 0011-3 Join the representation BE316
0 Comments
Explain two coding schemes. (4 marks)
Three ways used to represent negative number in binary number system
Using one’s complement, perform the following binary arithmetic leaving the answer decimal notation.19/7/2023 Using one’s complement, perform the following binary arithmetic leaving the answer decimal notation.  Describe the term prefixing an extra sign bit as used in data representation.
Two ways that may be used to represent a negative number in a number
Compute the value of x in the following expressions
(i) 24.3510 = X2 (3mks)
(ii) 6ABH = X10 (2mks)
Using twos complements compute the following using 8 bits binary (4mks)
2510 – 2010
c) Subtract the following binary numbers using the One’s Compliment method. (3mks)
(11101)2 – (1010)2
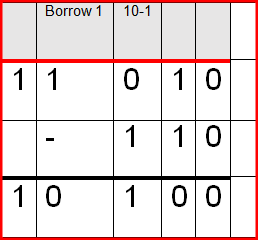
d)Convert 60578 to Hexadecimal. (3mks)
(a) Subtract 1102 from 110102 (1mk)
(b) Find the sum of binary number 101.1012 and 110.1002 (1mk)
(c) Convert binary number 11010110.10012 into octal number. (1mk)
Explain three functions of an information system in an organisation.
(b) Explain two benefits that a company would gain from using batch processing method for data processing
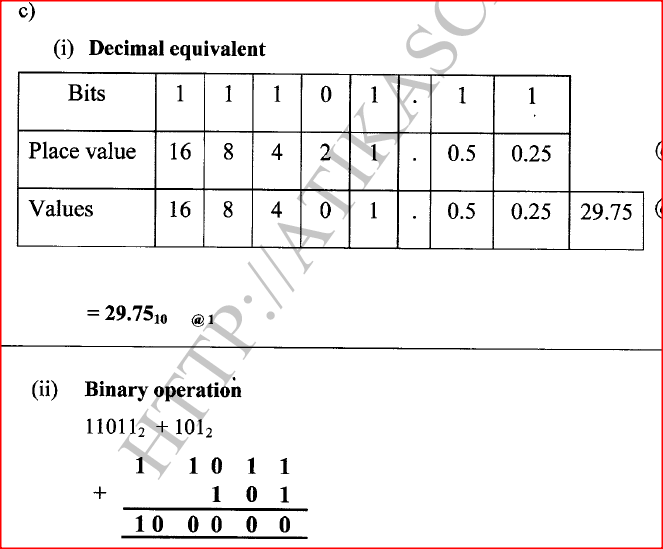
(c) (i) Convert the number 11101.1 12 to its decimal equivalent.
(ii) Perform the following binary operation 110112 + 1012
RESPONSES
a) Functions of information system in an organization.
Explain two health issues that could arise from the use of unsuitable computer desk.
Determine how the number 0.3125 base 10 would be represented. 
Convert each of the following binary numbers to decimal equivalent given that the left most digit is a sign bit:
(a) 00101101
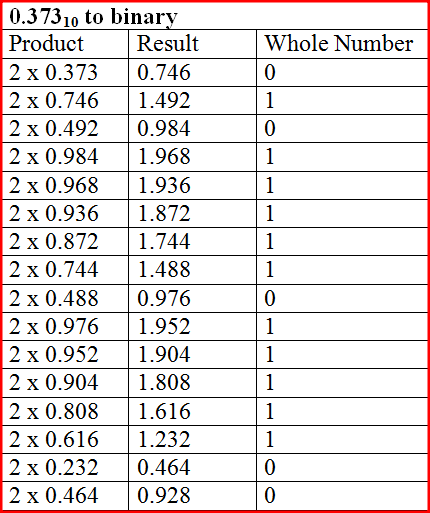
(b) 11001001 
Convert the decimal number 20.373 to its binary number system equivalent. (3 marks)
Converting 20 base 10 into binary
since the result was long, we just decided to truncate at 16th digit however it can exceed
0.37310 = 01011111011111002The binary result of 20.37310 is therefore
Combine them all;
In the BCD number coding scheme, letter A is represented by 110001 and letter B by 110010. Determine how the word CAB is coded in BCD.
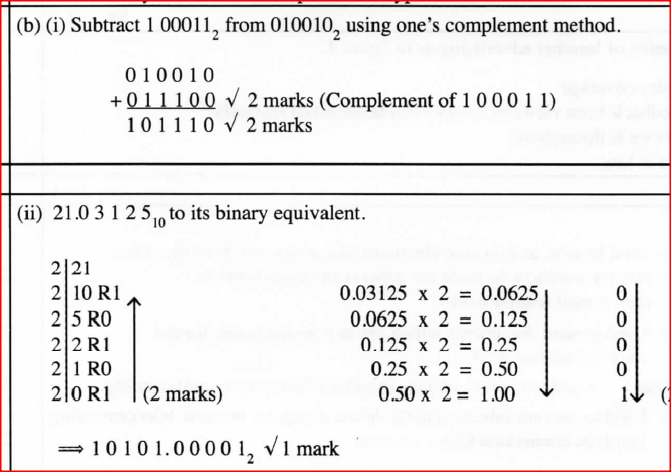
(ii) Convert the decimal number 11.125 to its binary number system equivalent.
(iii) Perform the binary arithmetic: 111.01 + 1011.111 — 101.011 and convert the answer to decimal notation. (b) Explain the importance of each of the following in word processing: (i) tab stops; (ii) section breaks. (c) State three documents that are used during mail merging in word processing.
ANSWERS
(b) Importance of tab stops and section break
Describe the octal number system.(a) Describe the octal number system. (b) Convert each of the following to the number system indicated: (i) 111.1012 to decimal;(ii) 14.687510 to binary.(c) Convert the number -17 10 into 8-bit: (i) signed magnitude representation;(ii) two’s complement.(d) Perform the arithmetic operation 110.112 + 11.0112
RESPONSES
(a) Characteristics of octal number system.
Given the binary number 101011101111011, determine the number of:nibbles and bytes.
Related Searches on data representation in a computer, Form 3 LevelA) Explain three features of a graphical user interface as used in computers. (6 marks)
B) State the function of each of the following computer keyboard keys:
(i) Caps Lock (1 mark)
(ii) Shift (1 mark) (iii) Home (1 mark)
(i) Function of Caps lock
- It’s a toggle key when ON, the characters typed are in uppercase when OFF, the characters typed are in lower case. (ii) Shift key - Used to enable uppercase letter to be printed when alphanumeric keys are pressed. - Used with other keys to modify behavior/function key. (iii) Home key - Used to take the cursor to the beginning of the line in a word processor. - Evidence of movement of the cursor. C) Using two complement notation, determine the value of the operation 2510 — 2910 (6 marks)
Differentiate between one’s complement and two’s complement in data representation.
(a) (i) Differentiate between one’s complement and two’s complement in data representation.
(ii) Explain the preference of binary number systems over decimal number systems in computers. (b) (i) Using one’s complement, subtract 1000112 from 0100102 (ii) Convert the number 21.0312510 to its binary equivalent. (c)Perform the following binary operations. 1101 + 11011 + 101 + 11111
State the use of each of the following flowchart symbols.
(a) Convert each of the following binary numbers to decimal equivalent given that the left most digit is a sign bit.
(î) 0 0 1 0 1 1 0 1 (ii) 1 1 0 0 1 0 0 1 (b) Convert the decimal number 0.42 to 6 bit binary notation. (c) Using two’s complement, subtract 1110 from 810 leaving your answer in binary notation. (d) Perform the following binary operation. 11001 + 1101-101 RESPONSES
(a) Describe each of the following validation checks as used in data processing:(i) Preserve checkIt is a measure placed used to ensure that data item is in its original status. (ii) Data type checkIt is a measure that ensures that correct data type is entered for each field. (iii) Check digitThis is a number calculated by the computer to make sure that the other numbers in a sequence have been entered properly. 
State three standard data coding schemes used in computing and electronic systems.
(b) Convert each of the following numbers:
(i) 110.1012 to decimal; (ii) 12.687510 to binary; (c) Subtract 110.012 from 11001.01012 (d) Using twos complement, perform the following binary arithmetic leaving the answer in binary notation. 11012- 1001012
(a) Binary coded Decimal (BCD) )(4 bits).
Using ones complement, convert the decimal number -9 into a 6-bit binary number.
(b) (i) State three standard coding schemes used in data representation.
(ii) In a certain coding scheme, each character occupies 7 bits. Letters of the alphabet are assigned consecutive codes. If letter N is represented by 1010010. What is the representation of letter A in this coding scheme? (c) Using twos complement. show how the arithmetic below would be carried out on a 8-bit computer system. (+54)- (+29) 
Perform the following binary arithmetic and give your answers in decimal notation:
(i)1010.101 + 11.011
(ii)1010.011 – 11.011 (b) Covert the following numbers into their binary equivalents (i)0.562510 (ii)0.312510 (c) Using four – bit twos compliment, perform the following arithmetic 1012- 1112 
(a) Subtract 01112 from 10012 (2 mks)00102 (b) Using two’s compliment, subtract 7 from 4 and give the answer in decimal notation (4mks)7 = 1112 4 = 1002 -4 in two’s compliment is 100 111 100 + (1)011 The resulting answer is 011 since the overflow is ignored. In decimal notation this is 310 (c) Convert(i) 91B16 to octal
|
Categories
All
Archives
December 2024
|
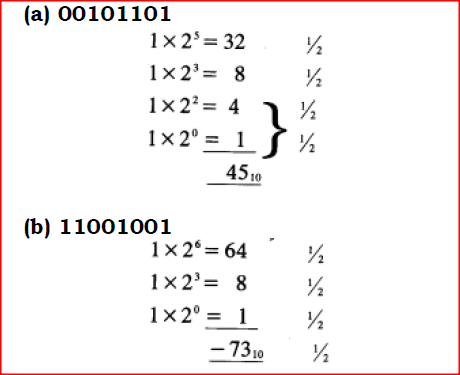
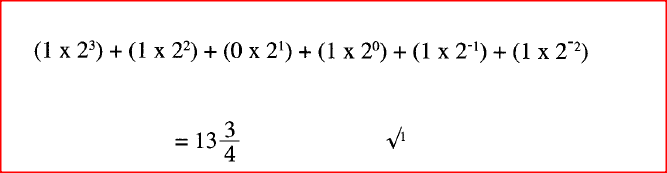
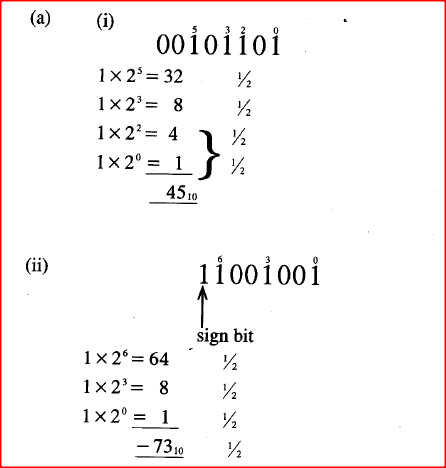
RSS Feed