K.C.S.E Biology Q & A - MODEL 2018PP2QN06
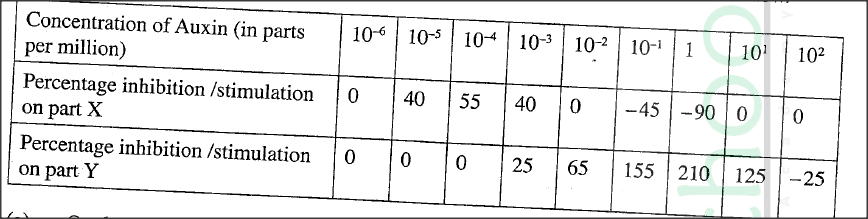
The effect of auxin concentration on growth response of two parts of a plant, X and Y was investigated over a period of time. The results were tabulated as shown in the table below.
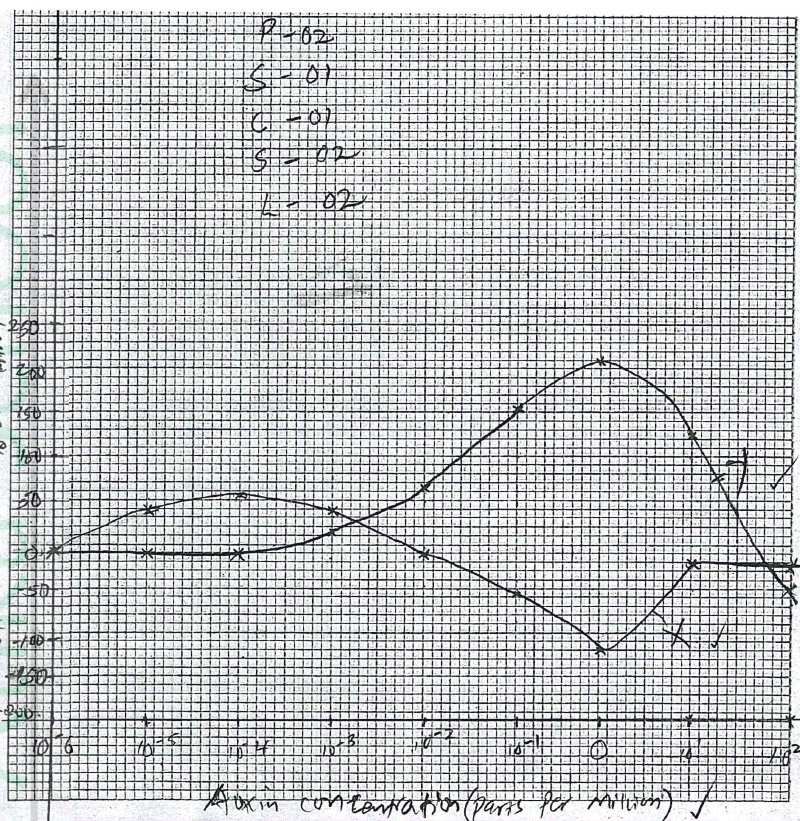
(a) On the same axis, draw line graphs of the effect on growth of the two parts, X and Y (percentage inhibition or stimulation) against the concentration
(b) With reasons, name the two parts of the plant, X and Y. X Reason Y Reason (c) From the graph identify: . (i) the point at which the percentage stimulation was the same for both X and Y. (ii) the optimum concentration of auxins required for part Y (d) State three ways in which the effects of auxins on plants is applied in flower farming. (e) Distinguish between simple and conditioned reflex action
answers
b) X—root;
Reason Low auxin concentration stimulates (rapid/faster) cell division and elongation/growth in roots; High concentration of auxins inhibits growth in roots; Y—shoot; Reason Low auxin concentration has little effect on the growth of shoots/shoots are stimulated to grow with high auxin concentration (up to a given optimum); c) i. 33%±2; ii. 1.0 parts per million; (d)Faster maturity of flowers/earlier flower formation/flowering; Prunning/decapitating shoot tips to allow sprouting of lateral buds, hence more yield; Keeping flowers fresh; Stimulate formation/development of (adventitious) roots;
0 Comments
K.C.S.E Biology Q & A - MODEL 2018PP2QN02
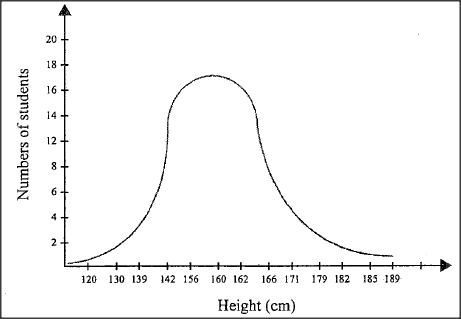
Below is a graphical representation of students’ height in a classroom.
(a) Name the type of curve illustrated.
(b) (i) State the type of variation represented by the curve. (ii) State two meiotic processes that lead to variation among organisms. (iii) Explain the role of variation in organisms. (c) Explain the need for genetic counselling in present day health facilities.
answers
a) Normal distribution curve;
b) i. Continuous (variation); ii. Independent assortment; Crossing over; iii. Organisms/individuals with advantageous traits/variations are favoured/selected by nature; and survive to reproduce/pass on/propagate the advantageous/favourable traits to their off-spring; Or Variation ensures propagation of desirable/favourable traits; to the future generations/off-spring, ensuring improved/quality population; c) Provides information/advice to individuals/families/communities about genetic disorders; Helps identify/test/advice families/communities on possible risks of genetic disorders; Provides supportive services/serves as patient advocates/refer individuals/families to relevant health professionals; K.C.S.E Biology Q & A - MODEL 2018PP1QN23
State two characteristics of living things illustrated in the photograph below.
answers
K.C.S.E Biology Q & A - MODEL 2018PP1QN14
The diagram below illustrates a germinating seedling.
(a) Name the type of germination illustrated in the diagram
(b) Describe how the type of germination named in (a) above is brought about.
answers
(a) Epigeal;
(b) Hypocotyl elongates faster than the epicotyl; pushing cotyledons above the ground;
K.C.S.E Biology Q & A - MODEL 2018PP1QN13
State two limitations of using a quadrat to estimate the population of organisms.
ANSWERS
K.C.S.E Biology Q & A - MODEL 2017PP2QN07
Explain the importance of protecting the forest ecosystem with reference to the following:
(a) climate change (b) biodiversity (c) biotechnology (d) water conservation (e) pollution.
answers
a) Climate change
Name the hormone responsible for the development of secondary sexual characteristics in human males.1/7/2020
K.C.S.E Biology Q & A - MODEL 2017PP2QN04
Name the hormone responsible for the development of secondary sexual characteristics in human males.
answer
K.C.S.E Biology Q & A - MODEL 2017PP2QN04
State the significance of diploidy.
answers
K.C.S.E Biology Q & A - MODEL 2017PP2QN04
(i) Define the term diploidy.
(ii) Name the type of cell division that gives rise to diploid cells. (iii) Name the type of cells in which the process named in (b) (ii) above Occurs.
answers
i. State of being/having two sets of chromosomes and therefore two copies of genes (especially in somatic/body cells);
ii. Mitosis; iii. Body cells/somatic cells;
K.C.S.E Biology Q & A - MODEL 2017PP2QN04
Explain how the sex of a male child is determined in human beings.
answers
K.C.S.E Biology Q & A - MODEL 2017PP1QN14
The photograph below illustrates a germinating seedling.
(a) Name the type of germination illustrated in the photograph.
(b) Explain the function of each of the parts labelled G and H. G H
answers
a. Epigeal;
b. G- Elongates to expose the foliage leaves to light photosynthesis H- Stores food (for growth); For photosynthesis (it is green); Protects plumule during germination; K.C.S.E Biology Q & A - MODEL 2017PP1QN07
The diagram below represents a stage in the division of a cell.
With a reason, identify the organism from which the cell was obtained.
answers
K.C.S.E Biology Q & A - MODEL 2017PP1QN05
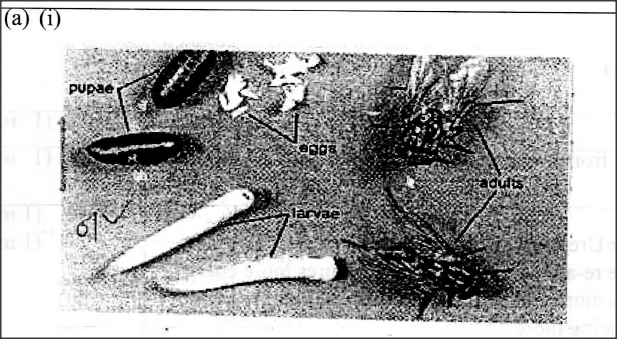
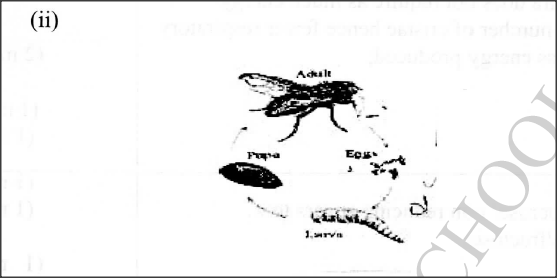
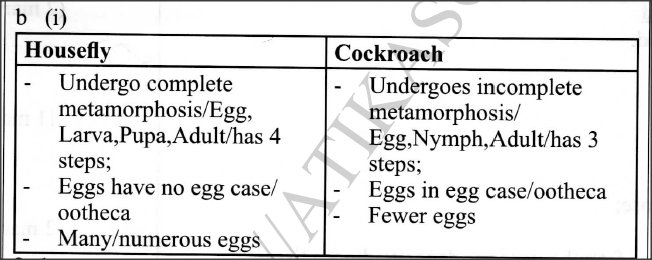
The photograph illustrates a housefly at various stages of its development.
(a) (i) On the photograph, name the stages of the life cycle.
(ii) Using arrows, link the stages of the life cycle in the correct order. (b) (i) State two differences between the life cycles of a housefly and that of a cockroach. (ii) State one advantage of the life cycle of a cockroach to itself. K.C.S.E Biology Q & A - MODEL 2016PP2QN01
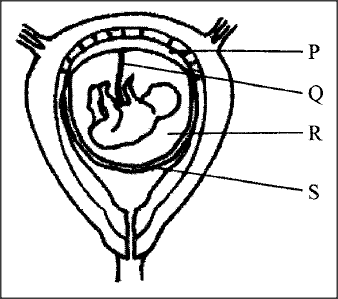
The diagram below represents a human foetus in a uterus.
(a) Name the part labeled S.
(b) (i) Name the types of blood vessels found in the structure labaled Q. (ii) State the difference in composition of blood found in the vessels named in (b) (i) above. c)Name two features that enable the structure labeled P to carry out its function. (d) State the role of the part labeled R.
ANSWERS
K.C.S.E Biology Q & A - MODEL 2016PP1QN30
State two advantages of hybrid vigour
ANSWERS
K.C.S.E Biology Q & A - MODEL 2016PP1QN21
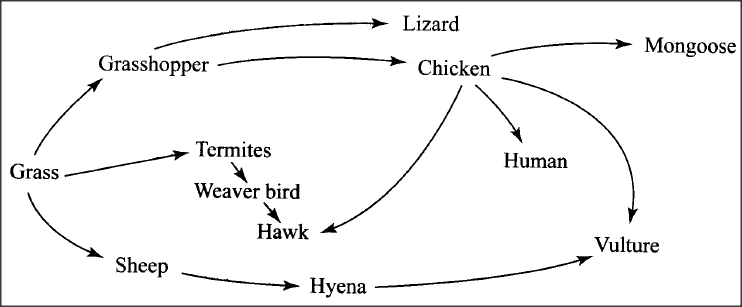
The figure below illustrates a food web in a certain ecosystem.
From the food web:
(a) Draw the shortest food chain (b) Identify the organism with the highest: (i) number of predators (ii) biomass
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN20
State three factors that contribute to the deceleration phase in the population curve of an organism.
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN15
What is seed dormancy
answer
K.C.S.E Biology Q & A - MODEL 2016PP1QN12
Other than using the quadrant, give two methods of estimating population of grass.
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN11
Name two benefits that a parasite derives from the host
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN10
State two functions of the placenta in mammals.
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN10
State two disadvantages of sexual reproduction in animals.
answers
K.C.S.E Biology Q & A - MODEL 2016PP1QN07
Explain how the following prevent self-pollination.
(i) Protandry (ii) Self- sterility.
answers
K.C.S.E Biology Q & A - MODEL 2015PP2QN07
Explain the various ways in which seeds and fruits are adapted to dispersal.
ANSWERS
Wind - dispersed seeds / fruits are light / small to be carried by air currents;
Some seeds / fruits have developed hairy structure feather-like projections; wing like structure which increase their surface area to be blown about /carried away by wind; open capsules; borne on long stalks, which are swayed by wind scattering seeds. Water - dispersed fruits / seeds are also light; to float on water; Some, (like coconuts) have fibrous /spongy mesocarps to trap air; making them buoyant/floating on water; Others (like the water lily) produce seeds whose seed coats trap air bubbles; making them float on water; Some have water-proof seed testa / pericarp; remain afloat without soaking /sinking immediately they are released from parent plants; Animal - dispersed fruits have developed hooks; to stick on (the fur of passing) animals; In some cases, fruits are succulent, brightly coloured / scented; to attract animals, birds; The seed coats (of some seeds) are hard; and resistant to the digestive enzymes; hence passing out through the gut undigested; Self dispersal by explosive mechanism; Fruits have sutures/lines of weakness; which split open when drying scattering seeds. |
Archives
December 2024
Categories
All
TOPICSFORM 1
Form 2
Form 3
Form 4
|
Can't find what you are looking for? Don't worry, Use the Search Box Below.
|
Primary Resources
College Resources
|
Secondary Resources
|
Contact Us
Manyam Franchise
P.O Box 1189 - 40200 Kisii Tel: 0728 450 424 Tel: 0738 619 279 E-mail - sales@manyamfranchise.com |












 RSS Feed
RSS Feed

