KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
|
0 Comments
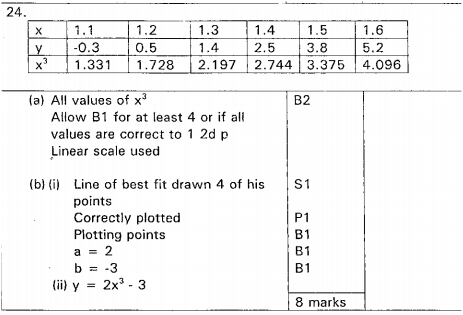
Data collected form an experiment involving two variables X and Y was recorded as shown in the table below.The variables are known to satisfy a relation of the form y = ax3+ b where a and b are constants
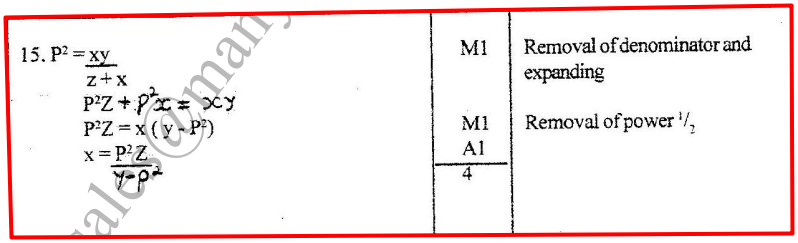
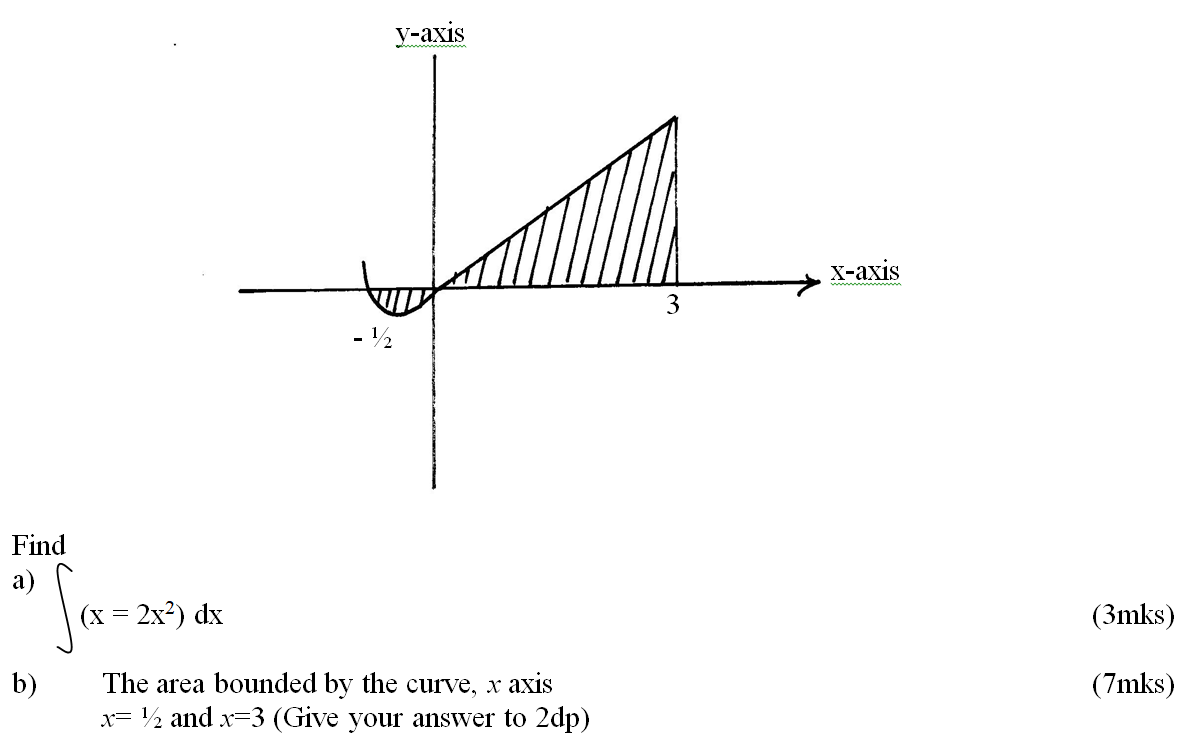
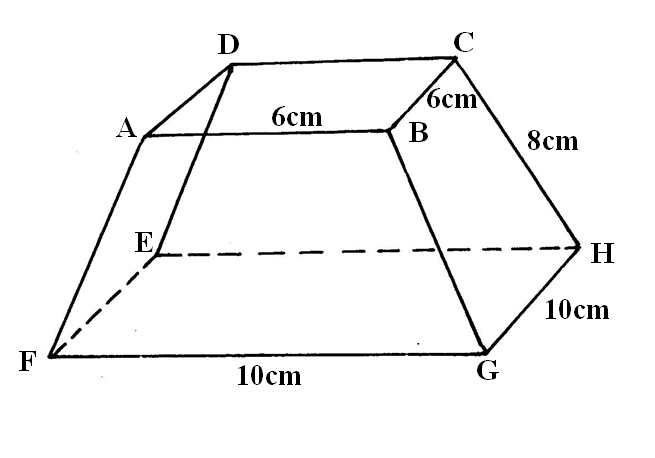
Two variables P and L are such that P varies partly as L and partly as the square root of L. Determine the relationship between P and L when L = 16, P = 500 and when L = 25, P = 800.5 marks A tailor makes two types of garments A and B. Garment A requires 3 metres of material while garment B requires 2 ½ metres of material. The tailor uses not more than 600 metres of material daily in making both garments. He must make not more than 100 garments of type A and not less than 80 of type B each day.(a). Write down all the inequalities from this information. (3mks)b) Graph the inequalities in (a) above (3mks)c) If the business makes a profit of shs. 80 on garment A and a profit of shs. 60 on garment B, how many garments of each type must it make in order to maximize the total profit? (4mks)Fill in the table below to 2 decimal places for the graph of y = sin x and y = 2sin (x-30) for the range – 180 £ x £180 (2mks)The curve of the equation y = x+ 2x2, has x = ½ and x = 0 as x-intercepts. The area bounded by the x-axis, x = ½ and x = 3 is shown by the sketch below.The table below shows income tax rates
|
|
Marks |
10-19 |
20-29 |
30-39 |
40-49 |
50-59 |
60-69 |
70-79 |
80-89 |
90-99 |
|
Frequency |
2 |
6 |
10 |
16 |
24 |
20 |
12 |
8 |
2 |
Using an assumed mean of 54.5, calculate the
a) Mean mark (4mks)
b) Variance (4mks)
c) Standard deviation (2mks)
(a) A and B are two points on earth’s surface and on latitude 400 N. The two points are on the longitude 500W and 1300E respectively. Calculate the distance from A to B along a parallel of latitude in kilometers. (2mks)
(b) The shortest distance from A to B along a great circle in kilometres (Take p = 22/7 and radius of the earth = 6370km) (2mks)
Seven people can build five huts in 30 days. Find the number of people, working at the same rate that will build 9 similar huts in 27days. (3mks)
A quantity P varies partly as Q and partly as the square root of Q, given that P=30 when Q=9, and P=14 when Q=16. Find P when Q=36. (3mks)
A carpenter wishes to make, a ladder with 18 cross-pieces. The cross pieces are to diminish uniformly in lengths from 65cm at the bottom to 31cm at the top. Calculate the length in cm, of the eighth cross-piece from the bottom. (3mks)
Categories
All
Algebraic Expressions
ALT B
Angle Properties Of A Circle
Angles And Plane Figures
Appreciation-and-depreciation
Approximation Errors
Area
Area Approximation
Area Of A Quadrilateral
Area Of Triangle
Area Part Of A Circle
Bearings
Binomial Expansion
BODMAS
Chords And Tangents Of A Circle
Commercial Arithmetic I
Commercial Arithmetic II
Common Solids
Compound Proportions
Decimals
Density Mass Weight
Differentiation
Divisibility Tests
Equation Of A Circle
Equations Of A Straight Line
Factorization
Factors
Form 1 Level
Form 2 Level
Form 3 Level
Form 4 Level
Formulae And Variations
Fractions
Further Logarithms
GCD HCF
Geometric Constructions
Gradients Of Curved Lines
Graphical Methods
Heros Formula
Income Tax
Indices Logarithms
Integers
Integration
Kcse-1995
Kcse-1995
KCSE 1996
KCSE 1997
Kcse1998
Kcse-1999
Kcse-1999
KCSE 2000
Kcse-2001
Kcse-2001
KCSE 2002
Kcse-2003
Kcse-2003
Kcse-2004
KCSE 2005
Kcse-2006
Kcse-2006
KCSE 2007
Kcse-2008
Kcse-2008
Kcse-2009
Kcse-2009
Kcse-2010
Kcse-2010
Kcse-2011
Kcse-2011
Kcse-2012
Kcse-2012
Kcse-2013
Kcse-2013
Kcse-2014
KCSE 2015
KCSE 2016
Kcse-2017
Kcse-2017
Kcse-2018
Kcse-2018
KCSE 2019
KCSE 2020
KCSE 2021
KCSE 2022
KCSE 2023
KCSE 996
LCM
Lengths
Linear Equations
Linear Inequalities
Linear Motion
Linear Programming
Loci
Longitudes And Latitudes
Mass
Matrices
Matrices And Transformations
Natural Numbers
Natural-numbers-and-prime-factors
Nets
Operation Of Numbers
Paper 1
Paper 2
Paper 2 Section A
Percentage
Perimeter
Probability
Pythagoras Theorem
Quadratic Expressions And Equations
Rates
Rates Ratio Proportion Percentage
Ratio
Reciprocals
Reflection And Congruence
Rotation
Scale Drawing
Section A
SECTION A PAPER 2
Section B
SECTION B PAPER 1
SECTION B PAPER 2
Sequences And Series
Similarity And Enlargement
Simple Surveying Techniques
Simultaneous Equations
Speed Distance Time
Squares And Square Roots
Statistics I
Statistics II
Surds
Surface Area Of Solids
Survey
Temperatures
Three Dimensional Geometry
Time
Trapezoidal Rule
Trigonometry I
Trigonometry II
Trigonometry III
Vectors I
Vectors II
Volume And Capacity
WAVES
Archives
December 2024
March 2024
February 2024
January 2024
December 2023
November 2023
June 2023
May 2023
April 2023
March 2023
January 2023
December 2022
December 2021
November 2021
October 2021
December 2020
September 2020
August 2020
July 2020
June 2020
May 2020
Latest Posts
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|
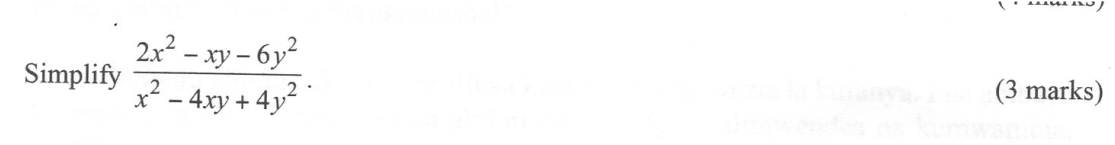

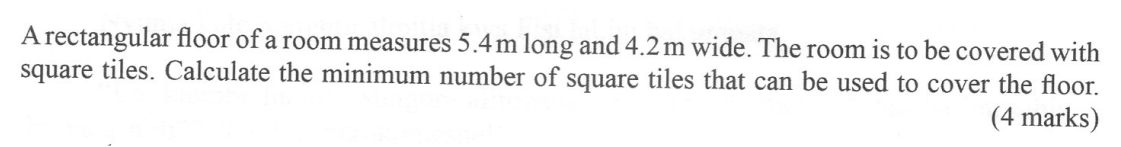
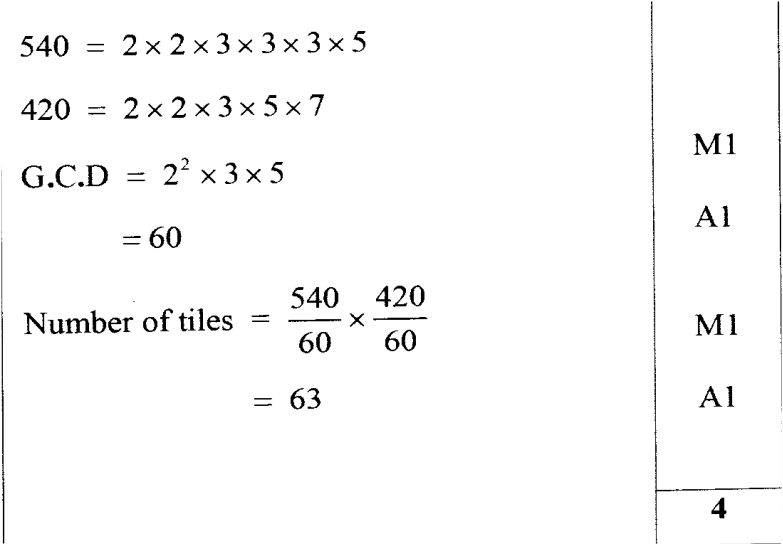

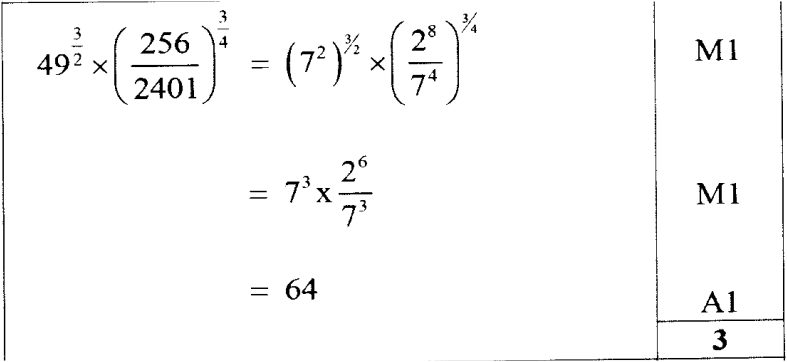











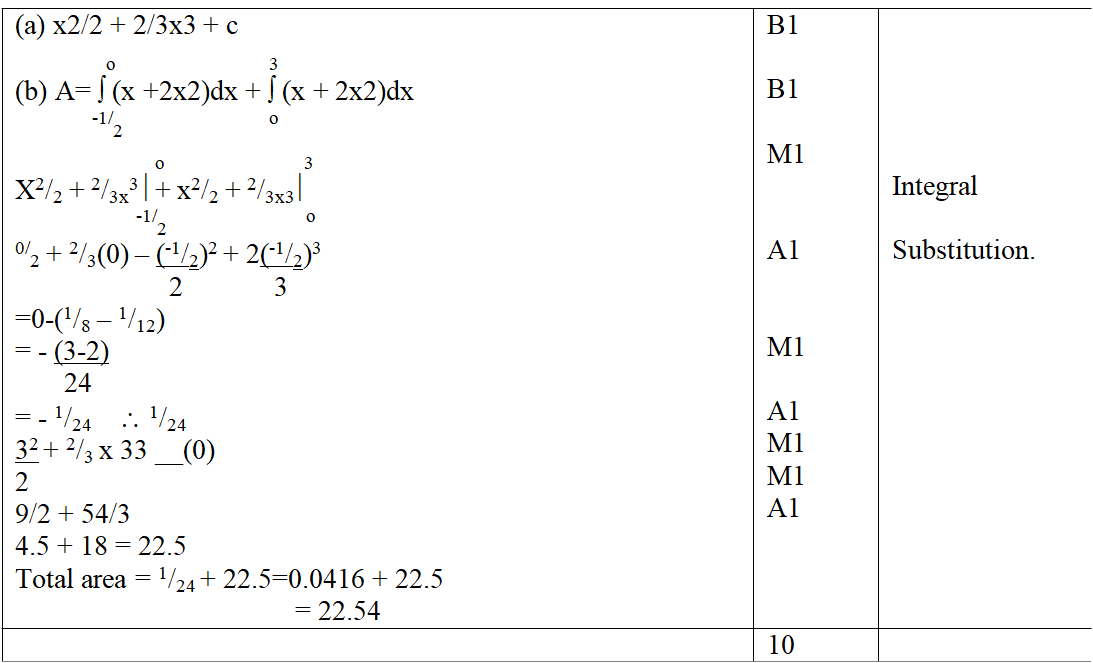


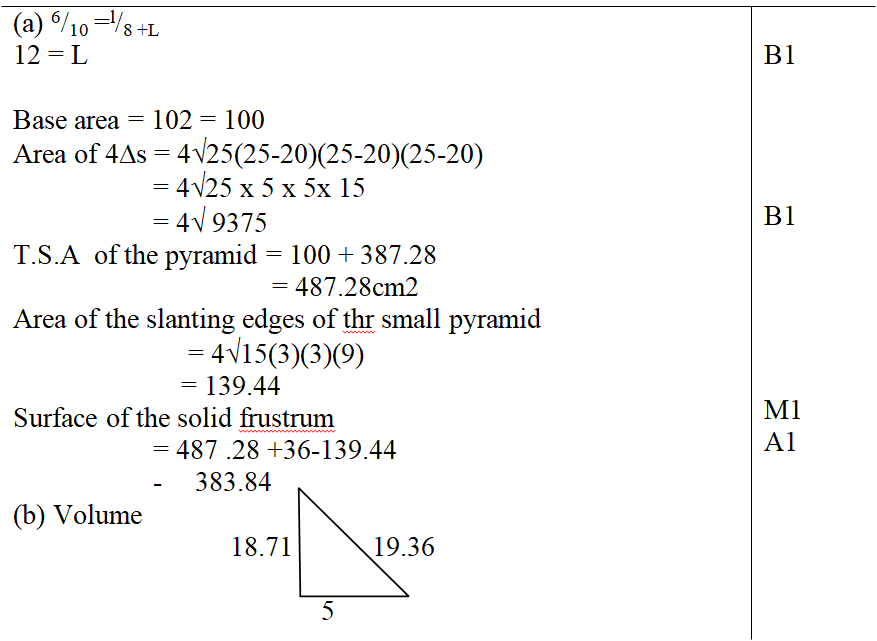

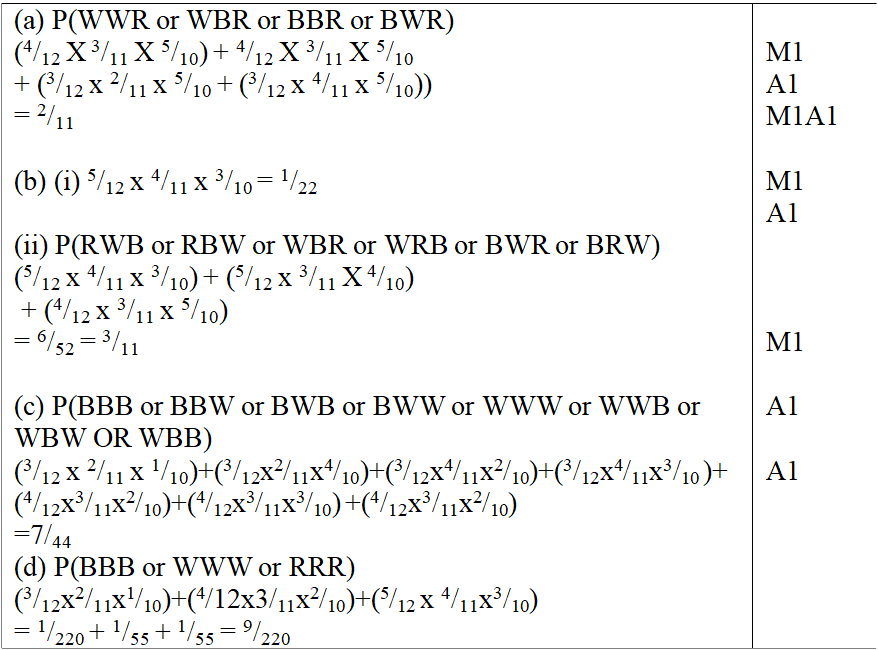












 RSS Feed
RSS Feed