KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
Form 3 Mathematics
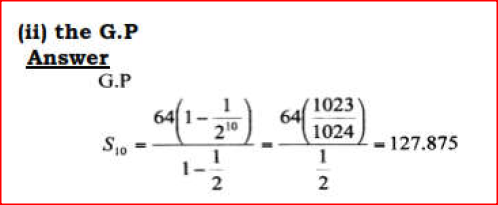
The first, fifth and seventh terms of an arithmetic progression (AP) correspond to the first three consecutive terms of a decreasing Geometric Progression (G.P.)
The first term of each progression, is 64, the common difference of the AP is d and the common ratio of the G.P. is r a i) Write two equation involving d and r ii) Find the values of d and r (4 mks) b) Find the sum of the first 10 terms of i) The arithmetic progression(A.P); ii)The Geometric Progression (G.P)
0 Comments
Form 4 Mathematics
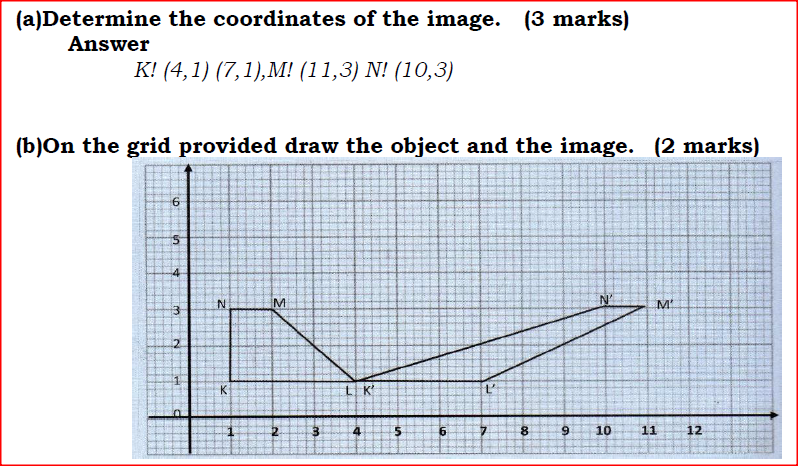
A quadrilateral with vertices at K (1, 1), L (4, 1), M (2, 3) and N (1, 3) is transformed by a matrix
a) Determine the coordinates of the image
(b)On the grid provided draw the object and the image. c)i)Describe fully the transformation which maps KLMN onto K’L’M’N ii) Determine the area of the image d) Find a matrix which maps K’L’M’N’ onto KLMN. Form 4 Mathematics
The gradient function of a curve is given by the expression 2x + 1. If the curve passes through the point ( -4, 6);
a)Find i)The equation of the curve ii)The value of x at which the curve cuts the x – axis b) Determine the area enclosed by the curve and the x – axis Form 4 Mathematics
A tourist took 1 hour 20 minutes to travel by an aircraft from town T(3°S, 35°E) to town U(9°N, 35°E, ). (Take the radius of the earth to be 6370km and π = 22/7)
(a) Find the average speed of the aircraft. (a) After staying at town U for 30 minutes, the tourist took a second aircraft to town V(9°N, 5°E), The average speed of the second aircraft was 90% that of the first aircraft Determine the time, to the nearest minute, the aircraft took to travel from U to V. (c) When the journey started at town T, the local time was 0700h. Find the local time at V when the tourist arrived. Form 1 Mathematics
A water vendor has a tank of capacity 18 900 litres. The tank is being filled with water from two pipes A and B which are closed immediately when the tank is full. Water flows at the rate of 150 000cm3/minute through pipe A and 120 000 cm3/ minute through pipe B.
(a) If the tank is empty and the two pipes are opened at the same time, calculate the time it takes to fill the tank (b) On a certain day the vendor opened the two pipes A and B to fill the empty tank. After 25 minutes he opened the outlet tap to supply water to his customers at an average rate of 20 litres per minute. (i) Calculate the time it took to fill the tank on that day. (ii) The vendor supplied a total of 542 jerricans, each containing 25 litres of water, on that day. If the water that remained in the tank was 6300 litres, calculate, in litres, the amount of water that was wasted. Form 4 Mathematics
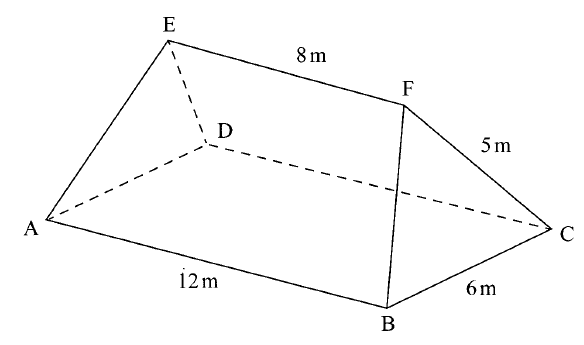
The figure ABCDEF below represents a roof of a house AB= DC = 12m, BC=AD = 6 m, AE=BF = CF = DE = 5 m and EF= 8m
a) Calculate correct to 2 decimal places, the perpendicular distance of EF from the plane ABCD
b) Calculate the angle between i)The planes ADE and ABCD ii)The line AE and the plane ABCD, correct to 1 decimal place iii)The planes ABFE and DCFE, correct to 1 decimal place. Form 3 Mathematics
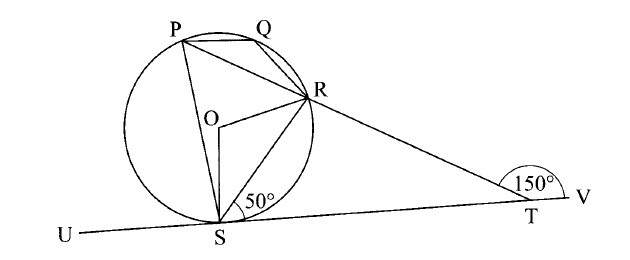
In the figure below, P, Q, R and S are points on the circle with centre O. PRT and USTV are straight lines. Line USTV is a tangent to the circle at S. Z.
RST = 50° and Z. RTV = 150°.
a) Calculate the size of
i)<QRS ii)<USP iii)<PQR b) Given that RT = 7 cm and ST = 9 cm, calculate to 3 significant figures i)Length of line PR ii)The radius of the circle Form 1 Mathematics
A garden measures 10 m long and 8 m wide. A path of uniform width is made all round the garden. The total area of the garden and the path is 168 m2.
(a) Find the width of the path. b) The path is to be covered with square concrete slabs. Each corner of the path is covered with a slab whose side is equal to the width of the path. The rest of the path is covered with slabs of side 50cm. The cost of making each corner slab is Sh 600 while the cost of making each smaller slab is Sh 50. Calculate; (i) the number of the smaller slabs used. (ii) the total cost of the slabs used to cover the whole path. Form 3 Mathematics
Find in radians, the values of x in the interval 0c ≤ x ≤ 2πc for which 2 cos2x - sin x = 1. (Leave the answer in terms of π)
Form 2 Mathematics
A school decided to buy at least 32 bags of maize and beans. The number of bags of beans were Lo be at least 6. A bag of maize costs Ksh 2500 and a bag of beans costs Ksh 3 500, The school had Ksh 100 000 to purchase the maize and beans. Write down all the inequalities that satisfy the above information,
Form 3 Mathematics
A circle whose equation is (x - 1)2 + (y - k)2 = 10 passes through the point (2,5).
Find the value of k. Form 3 Mathematics
(a) Expand the expression (1 + 1/2 x)5 in ascending powers of x, leaving the coefficients as fractions in their simplest form.
(b) Use the first three terms of the expansion in (a) above to estimate the value of (1 1/20)5 Form 3 Mathematics
An arc 11 cm long, subtends an angle of 70° at the centre of a circle. Calculate the length, correct to one decimal place, of a chord that subtends an angle of 90°
at the centre of the same circle. Form 3 Mathematics
A bag contains 2 white balls and 3 black balls. A second bag contains 3 white balls and 2 black balls. The balls are identical except for the colours. Two balls are drawn
at-random, one after the other from the first bag and placed in the second bag. Calculate the probability that the 2 balls are both white. Form 3 Mathematics
The first term of an arithmetic sequence is — 7 and the common difference in 3
(a) List the first six terms of the sequence; (b) Determine the sum of the first 50 terms of the sequence. Form 2 Mathematics
The masses in kilograms of 20 bags of maize were:
90, 94, 96, 98, 99, 102, 105, 91, 102, 99, 105, 94, 99, 90, 94, 99, 98, 96, 102 and 105. Using an assumed mean of 96 kg, calculate the mean mass, per bag of the maize. Form 1 Mathematics
Kago deposited kshs 30000 in a financial institution that paid simple interest at the rate of 12% per annum. Nekesa deposited the same amount of money as Kago in
another financial institution that paid compound interest. After 5 years , they had equal amounts of money in the financial institutions. Determine the compound interest rate, to 1 decimal place for Nekesas deposit Form 4 Mathematics
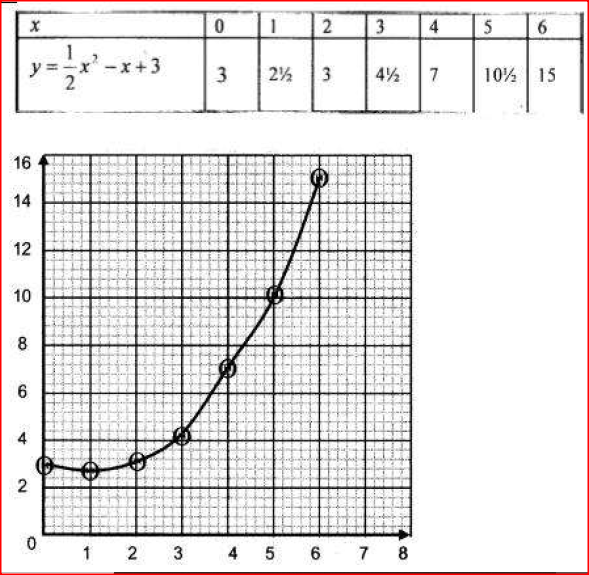
(a)On the grid provided, draw a graph of the function y = 1/2 x2 - x + 3 for 0 ≤ x ≤ 6.
b) Calculate the mid ordinates for five strips between x = 1 and x = 6, and hence use the mid- ordinate rule to approximate the area under the curve between x = 1, x = 6 and the x = axis c) Assuming that the area determined by integration to be the actual area, calculate the percentage error in using the mid ordinate rule |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|



















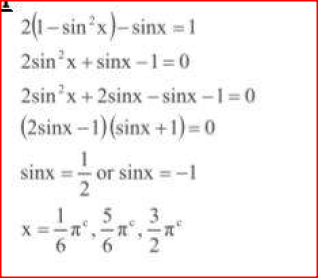



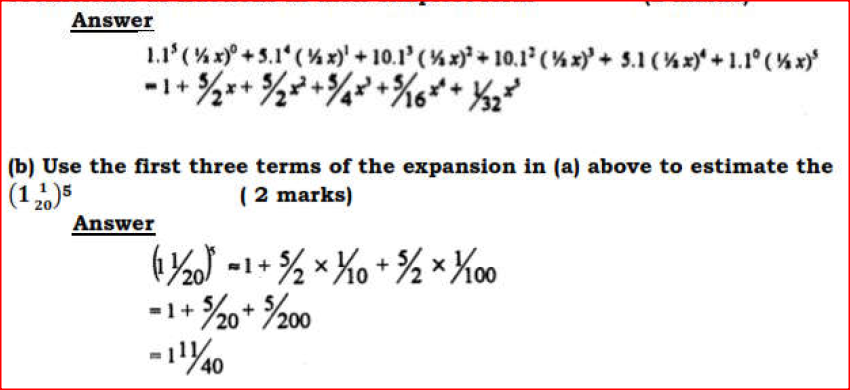
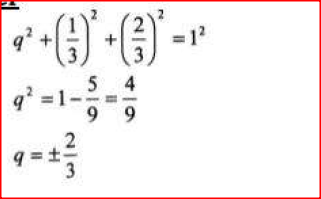





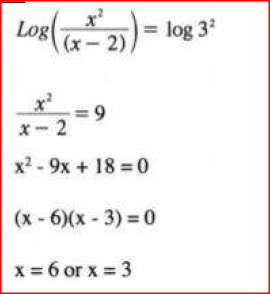








 RSS Feed
RSS Feed