KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
ALT B | AREA OF A RECTANGLE | SECTION 1 | QUESTION 4 | KCSE 2010 | FORM 2 LEVELThe length of a rectangular floor of a hall is 35.2m. If the diagonal of the floor is 37.7m, Calculate the area of the floor. (3 marks)
0 Comments
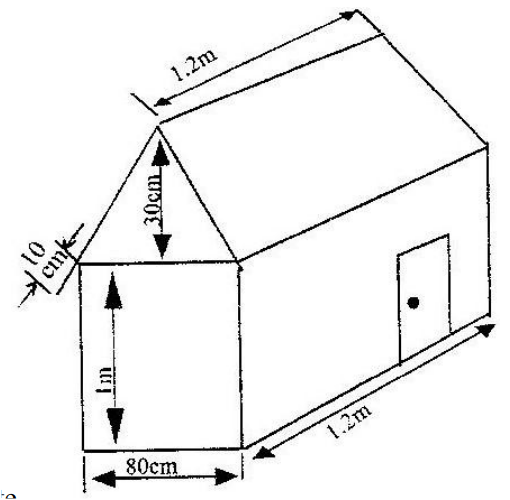
SURFACE AREA OF SOLIDS | KCSE 1997 | PAPER 1 | FORM 2 LEVEL | SECTION BThe figure below shows a portable kennel.
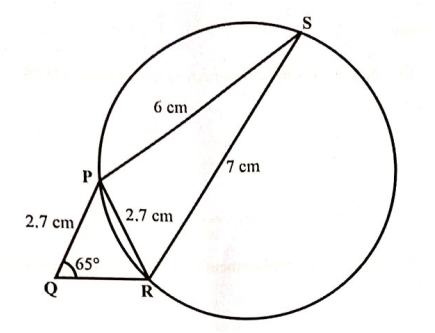
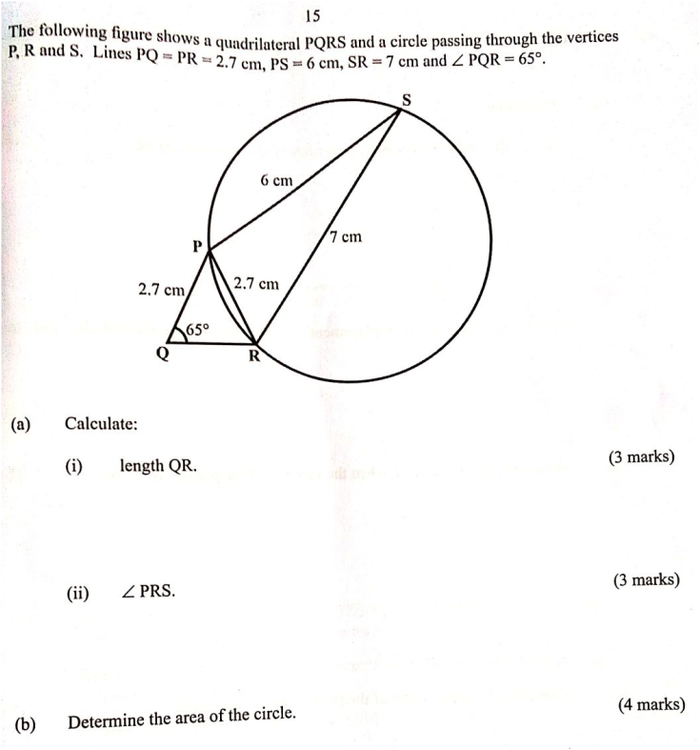
The following figure shows a quadrilateral PQRS and a circle passing through the vertices R and S29/12/2023 QUESTION 22 | KCSE 2023 | TRIGONOMETRY II | PAPER 1 | FORM 3 LEVELThe following figure shows a quadrilateral PQRS and a circle passing through the vertices R and S. Lines PQ = PR = 2.7 cm, PS = 6 cm, SR = 7 cm and ∠PQR = 65°.
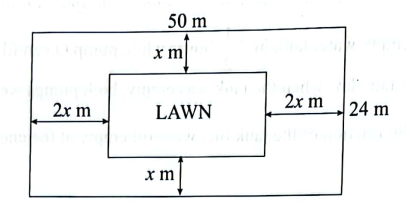
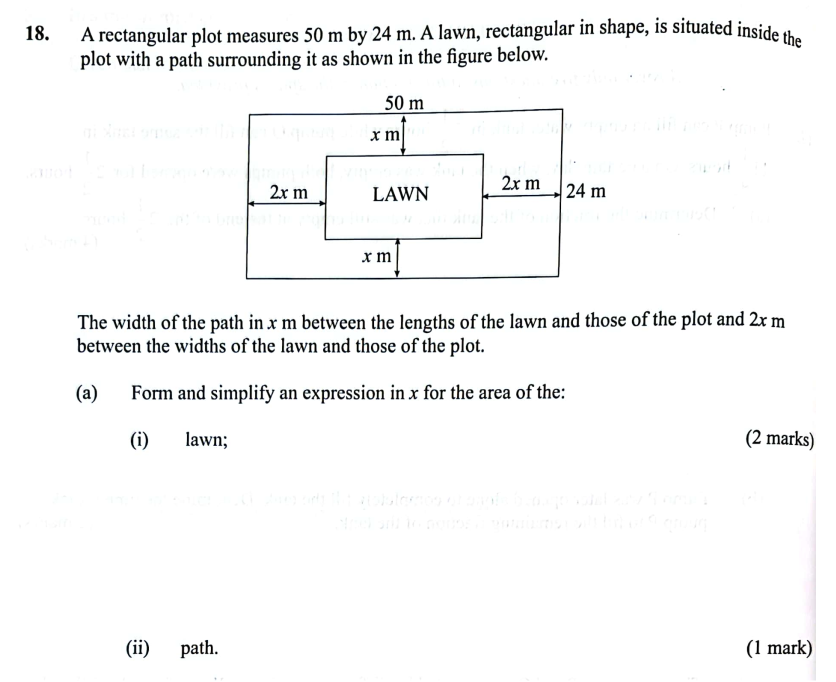
QUESTION 18 | KCSE 2021 | AREA | PAPER 2 | FORM 3 LEVELA rectangular plot measures 50 m by 24 m. A lawn, rectangular in shape, is situated inside the plot with a path surrounding it as shown in the figure below. The width of the path in x m between the lengths of the lawn and those of the plot and 2x m between the widths of the lawn and those of the plot.
A map has a scale of 1 : 2500 and on it is square plot of land which has an area of 4cm². Calculate the actual area in hectares of the land. (3mks)Worked Answer:Form 2 MathematicsForm 1 MathematicsForm 2 Mathematics
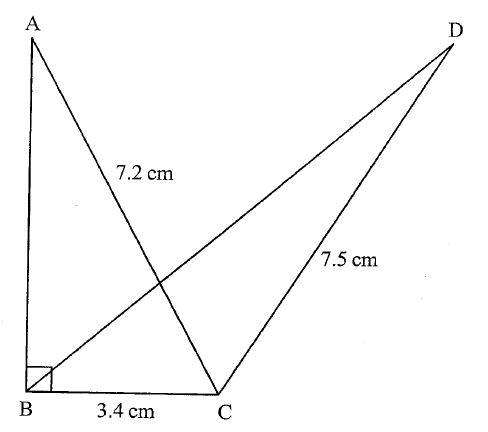
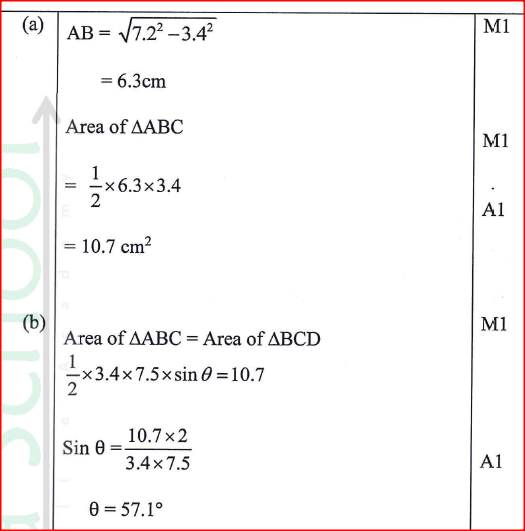
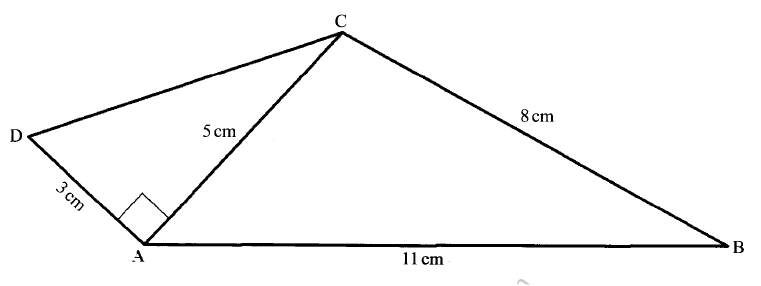
The figure below shows two triangles, ABC and BCD with a common base BC = 3.4 cm. AC = 7.2 cm, CD = 7.5 cm and ABC = 90°.
The area of triangle ABC = Area of triangle ∠BCD.
Calculate, correct to one decimal place:
(a) the area of triangle ABC; (b) the size of ∠BCD; (c) the length of BD; (d) the size of ∠BDC. Form 1 Mathematics
A photograph print measuring 24cm by 15 cm is enclosed in a frame. A uniform space of width x cm is left in between the edges of the photograph and the frame. If the area of the space i‹ 270cm2, find the value of x.
Form 2 MathematicsForm 2 Mathematics
The length of a room is 3 m shorter than three times its width. The height of the room is a quarter of its length. The area of the floor is 60 m2.
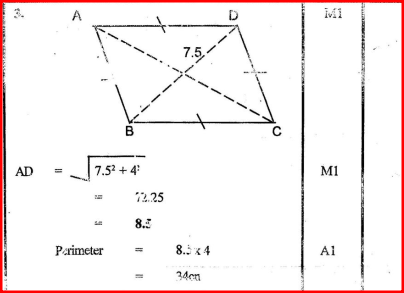
(a) Calculate the dimensions of the room. (b) The floor of the room was tiled leaving a border of width y m, all round. If the area of the border was 1.69m2, find: (i) the width of the border; (ii) the dimensions of the floor area covered by tiles. Form 2 MathematicsThe area of a rhombus is 60cm2. Given that one of its diagonals is 15 cm long, calculate the perimeter of the rhombus Form 4 MathematicsForm 1 Mathematics
A garden is in the shape of a right angled triangle. The length of the shortest side is l7 m and the area of the garden is 346.8 m2. Calculate the length of the longest side of the garden.
Form 2 MathematicsForm 1 Mathematics
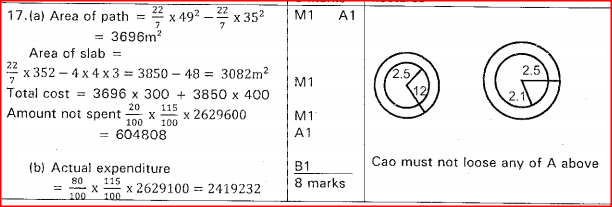
A garden measures 10 m long and 8 m wide. A path of uniform width is made all round the garden. The total area of the garden and the path is 168 m2.
(a) Find the width of the path. b) The path is to be covered with square concrete slabs. Each corner of the path is covered with a slab whose side is equal to the width of the path. The rest of the path is covered with slabs of side 50cm. The cost of making each corner slab is Sh 600 while the cost of making each smaller slab is Sh 50. Calculate; (i) the number of the smaller slabs used. (ii) the total cost of the slabs used to cover the whole path. Form 2 Mathematics
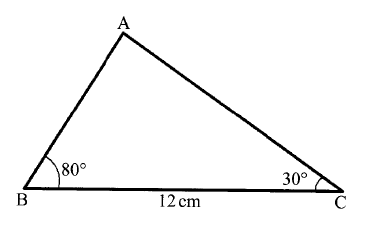
A triangular plot ABC is such that the length of the side AB is two thirds that of BC. The ratio of the lengths AB:AC = 4:9 and the angle at B is obtuse.
a) The length of the side BC
b)
i) The area of the plot
iii) The size of ∠ABC Form 1 Mathematics
The length and width of a rectangular signboard are (3x +12) cm and (x — 4) cm respectively.
If the diagonal of the signboard is 200cm, determine its area. Form 2 Mathematics
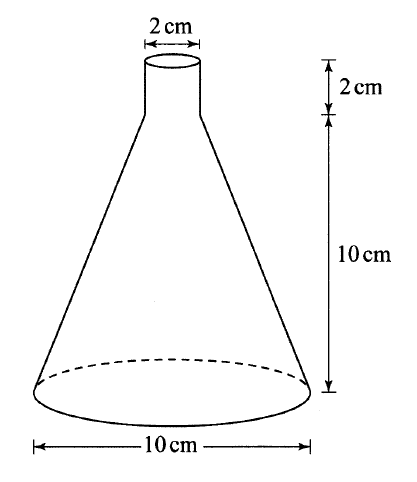
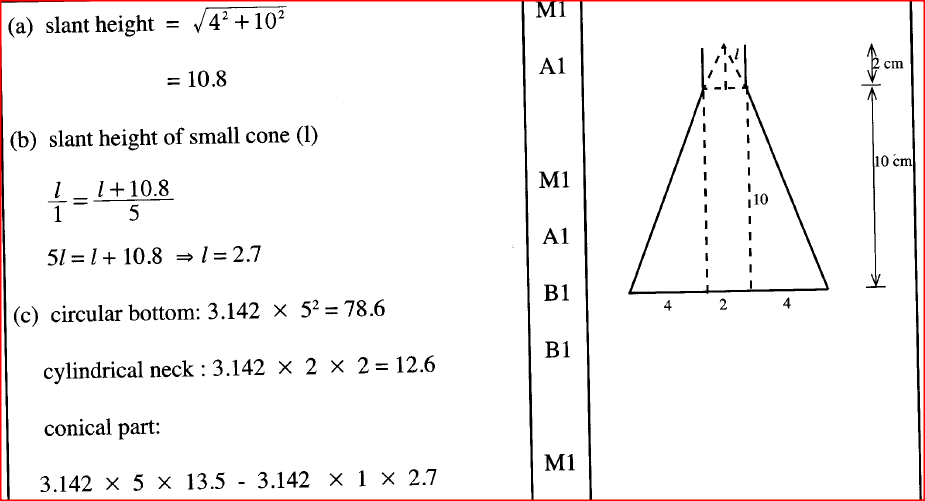
The figure below represents a conical flask. The flask consists of a cylindrical part and a frustum of a cone. The diameter of the base is 10cm while that of the neck is 2 cm. the vertical height of the flask is 12cm.
Calculate, correct to 1 decimal place
a) The slant height of the frustum part b) The slant height of the smaller cone that was cut off to make the frustum part c) The external surface area of the flask. (Take π =3.142) Form 1 Mathematics
A tailor had a piece of cloth in the shape of a trapezium. The perpendicular distance between the two parallel edges was 30cm. The lengths of the two parallel edges were 36 cm and 60cm. The tailor cut off a semi circular piece of the cloth of radius 14cm from the 60cm edge.
Calculate the area of the remaining piece of cloth. (Take π = 22/7) Form 2 Mathematics
The figure below shows a right pyramid VABCDE. The base ABCDE is regular pentagon. AO = 15cm and VO = 36 cm.
Calculate:
(a) The area of the base correct to 2 decimal places (b) The length AV (c) The surface area of the correct to 2decimal places (d) The volume of the pyramid correct to 4 significant figures Form 3 Mathematics
(a) solve the equation;
(b) The length of a floor of a rectangular hall is 9m more than its width. The area of the floor is 136m2.
i. Calculate the perimeter of the floor. ii. A rectangular carpet is placed on the floor of the hall leaving an area of 64m2. If the length of the carpet is twice its width, determine the width of the carpet. Form 2 MathematicsThe length of a room is 4 metres longer its width. Find the length of the room if its area is 32cm2 A company is to construct a parking bay whose area is 135m2. It is to be covered with concrete slab of uniform thickness of 0.15. To make the slab cement. Ballast and sand are to be mixed so that their masses are in the ratio 1: 4: 4. The mass of m3 of dry slab is 2, 500kg.
|
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|




























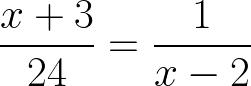

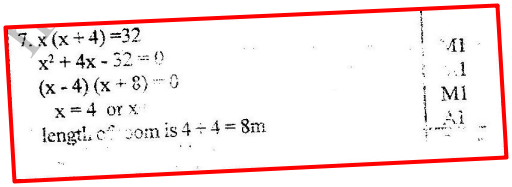



 RSS Feed
RSS Feed