KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
QUESTION 15 | KCSE 2023 | differentiation | PAPER 2 | FORM 4 LEVELThe gradient function of a curve is given by dy/dx = 3 - 4x. If the curve passes through the point (-1, 10), find the equation of the curve. (3 marks)
0 Comments
QUESTION 23 | KCSE 2023 | differentiation | PAPER 1 | FORM 4 LEVELThe displacement, x metres, of a particle moving a long straight line after t seconds is given by x = t³/3 - 3t² + 9.
QUESTION 15 | KCSE 2023 | DIFFERENTIATION | PAPER 1 | FORM 4 LEVELThe equation of a curve curve is given by y = 3x² - 2x. Determine the equation of a normal to the at x = 2. (4 marks)
QUESTION 24 | KCSE 2021 | DIFFERENTIATION | PAPER 1 | FORM 4 LEVELThe equation of a curve is given as y = 1/3 X^3 - 1/2X^2 - 2X - 1/3.
QUESTION 16 | KCSE 2021 | Differentiation | PAPER 1 | FORM 4 LEVELA curve is given by y = 2x³ - 3x² - 12x + 12. (1 mark)
(a) Find the gradient function of the curve. (b) Determine the equation of the normal to the curve at the point (1, -1), in the form y=mx+c, where m and c are constants. (3 marks) QUESTION 23 | KCSE 2022 | DIFFERENTIATION | PAPER 1 | FORM 4 LEVELA supermarket sold 530 packets of milk daily when the price was Ksh 50 per packet.
Whenever the price per packet was increased by Ksh 4, the number of packets sold daily decreased by 20. If n represents the number of times the price was increased: (a) write an expression in terms of n for: (i) the price of a packet of milk after the price was increased. (1 mark) (ii) the number of packets of milk sold after the price was increased. (1 mark) (iii) the total sales, in simplified expanded form, after the price of a packet of milk was increased. (2 marks) (b) Determine: (i) the number of times the price was increased to attain maximum sales. (3 marks) (ii) the price of a packet of milk for maximum sales. (1 mark) (iii) the maximum sales. (2 marks) the displacement, s metres of a moving particle after t seconds in given by
KCSE 2020 MATHEMATICS ALT A PAPER 1 QUESTION 24
​A particle moves along a straight line such that its displacement S metres from a given point is S = t^3-5t^2 + 3t + 4. where t is time in seconds.A particle moves along a straight line such that its displacement S metres from a given point is S = t3-5t2 + 3t + 4. where t is time in seconds.Finda) The displacement of the particle at t = 5 (2mks) b) The velocity of the particle when t = 5 (2mks) c) The value of t when the particle is momentarily at rest. (3mks) d) The acceleration of the particle when t = 2. (2mks)
The velocity V m/s of a particle in motion is given by V=3t2-2t+5.Calculate the distance travelled by the particle between t= 2 seconds and t = 6 seconds. (3 marks)
Form 4 Mathematics
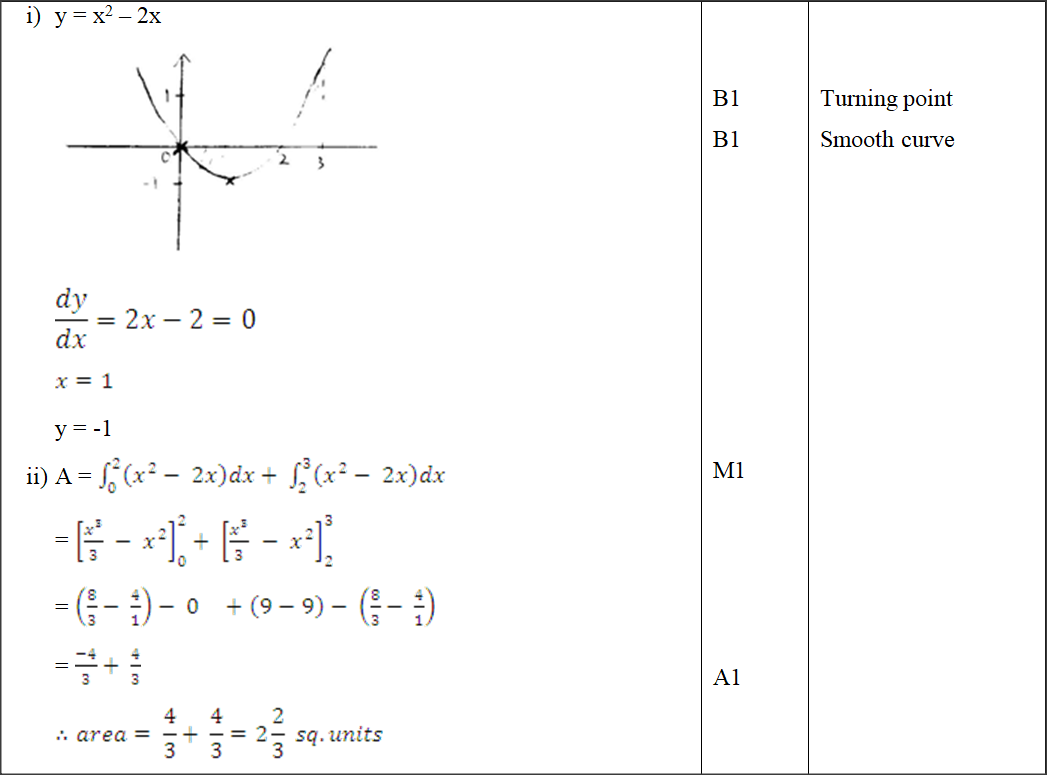
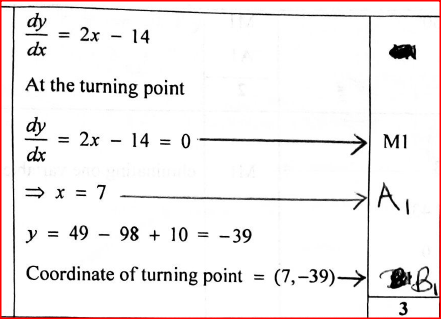
Find the coordinates of the turning point of the curve y= x²-14x +10
Form 4 Mathematics
The equation of a curve is y=x3+x2-x-1
(i) Determine the stationary point of the curve (Îi) the nature of the stationary points in (a) (i) above. (b) Determine: (i) the equation of the tangent to the curve at x = 1; (ii) the equation of the normal to the curve at x = 1. Form 4 MathematicsA curve is represented by the function y = 1/3 x3 + x2 – 3x + 2 (a) Find dy/dx (1 mark) (b) Determine the values of y at the turning points of the curve y = 1/3 x3 + x2 – 3x + 2 ( 4 marks) Form 4 Mathematics
The equation of a curve is given as y=1/3x3-4x+5
Determine: (a) The value of y when x = 3; (b) The gradient of the curve at x = 3; (c) The turning points of the curve and their nature. Form 4 Mathematics
The distance covered by a moving particle through point O is given by the equation, s = t3 - 15t2 + 63t — 10.
Find: (a) distance covered when t = 2 (b) the distance covered during the 3rd second; (c) the time when the particle is momentarily at rest; (d) the acceleration when t = 5. Form 4 MathematicsA stone is thrown vertically upwards from a point O After t seconds, the stone is S metres from O Given that S= 29.4t – 4.9t2, Find the maximum height reached by the stone ( 3 marks) Form 4 MathematicsThe gradient of a curve at point (x,y) is 4x – 3. the curve has a minimum value of – 1/8 (a) Find (i) The value of x at the minimum point ( 1 mark) (ii) The equation of the curve ( 4 marks) (b) P is a point on the curve in part (a) (ii) above. If the gradient of the curve at P is -7, find the coordinates of P ( 3 marks) Form 4 Mathematics
The equation of a curve is given as y = 2x3 -9/2 x2 -15x + 3.
(a) Find: (i) the value of y when x = 2; (ii) the equation of the tangent to the curve at x = 2. (b) Determine the turning points of the curve. Form 4 Mathematics
A particle moves in a straight line. It passes though point O at t = O with velocity v= 5m/s. The acceleration a m/s2 of the particle at time t seconds after passing through O is given by a = 6t + 4
(a) Express the velocity v of the particle at time t seconds in terms of t (b) Calculate (i) The velocity of the particle when t = 3 (ii) The distance covered by the particle between t = 2 and t = 4 Form 4 Mathematics
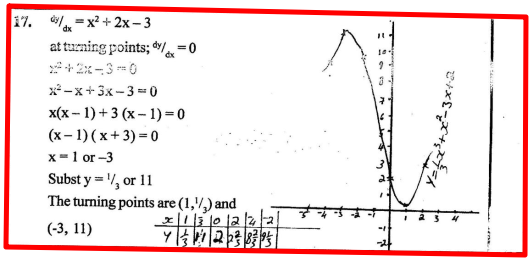
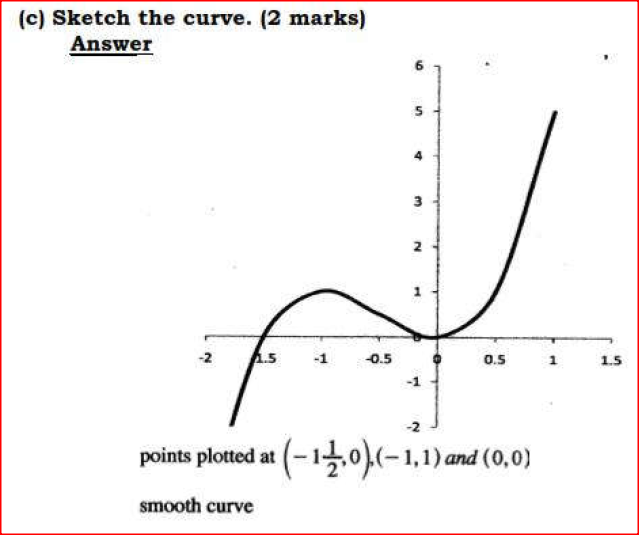
The equation of a curve is y = 2x3 + 3x2.
a)Find i)The x – intercept of the curve ii) they-intercept of the curve b i)Determine the stationary points of the curve ii)For each point in (b) (i) above, determine whether it is a maximum or a minimum c) Sketch the curve. Form 4 Mathematics
The gradient of the tangent to the curve y = ax3 + bx at the point (1,1) is -5 , Calculate the values of a and b.
Form 4 Mathematics
A particle was moving along a straight line. The acceleration of the particle after t seconds was given by (9 -3t) ms-2. The initial velocity of the particle was 7 ms-1.
Find: a) the velocity (v) of the particle at any given time (t); b) The maximum velocity of the particle; c)the distance covered by the particle by the time it attained maximum velocity |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|
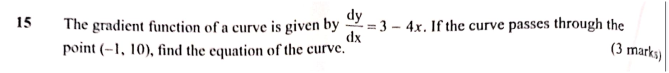
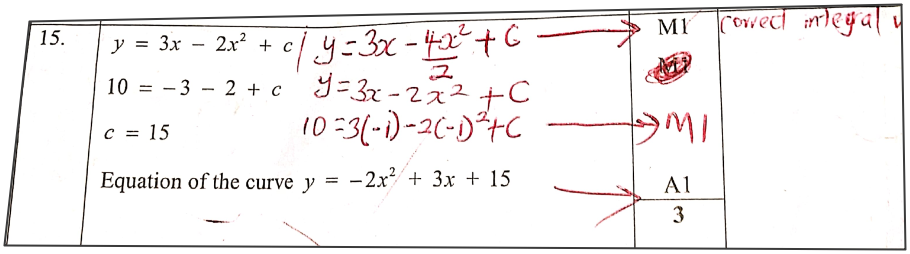



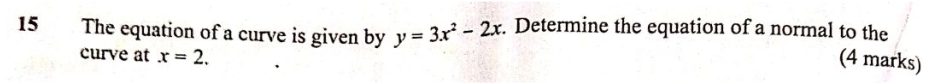












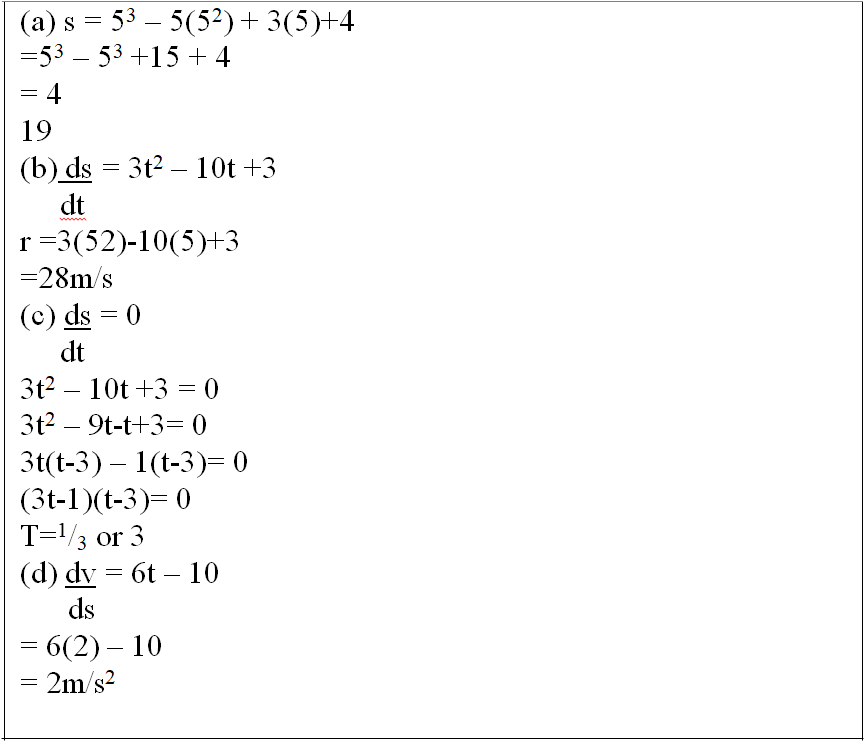

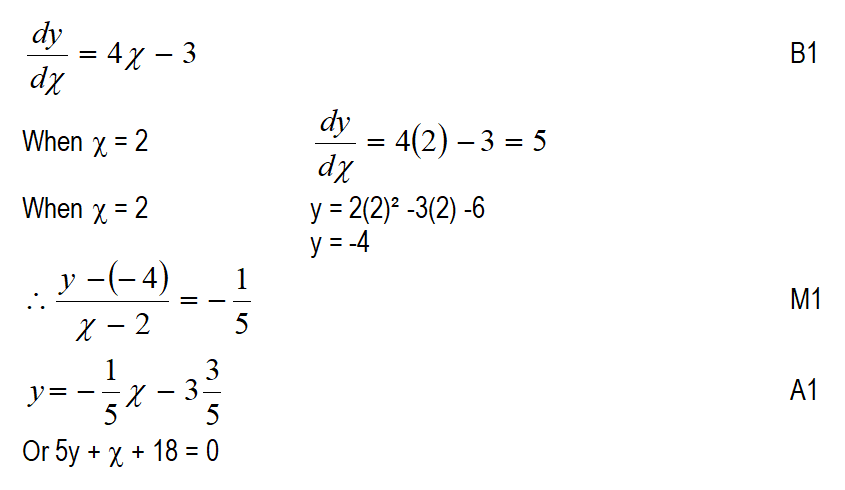



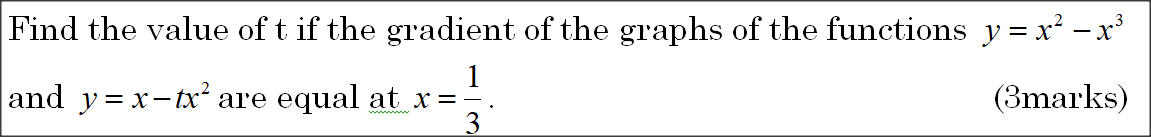

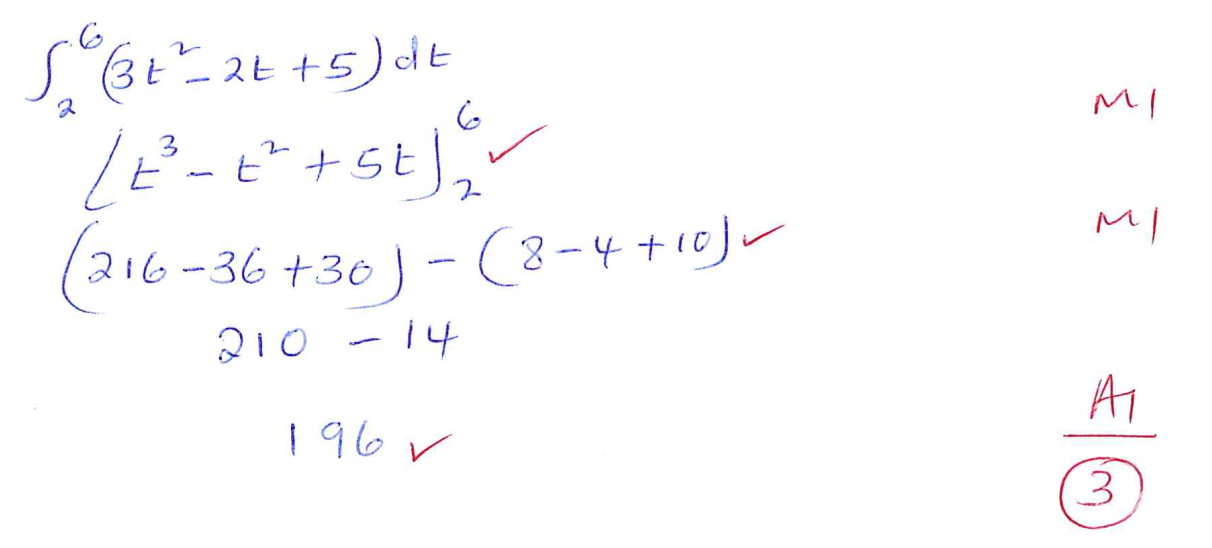
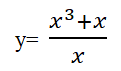


















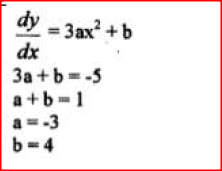

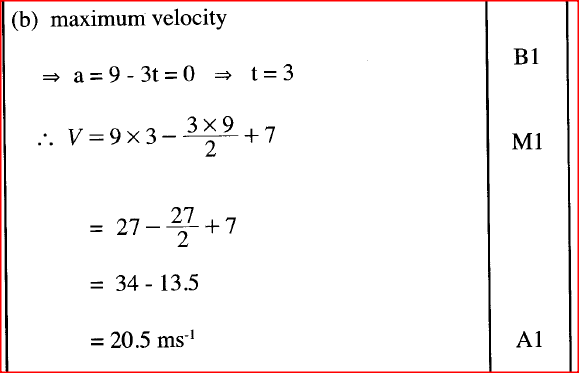
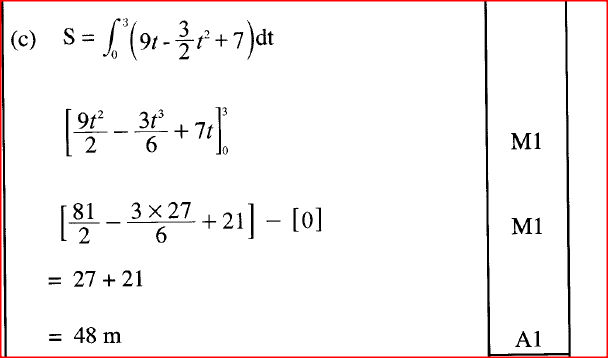

 RSS Feed
RSS Feed