KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
ALT B | LONGITUDES AND LATITUDES | | FORM 4 LEVEL | SECTION 1 | PAPER 2 | KCSE 2010 | QUESTION 14The positions of two points A and B on the surface of the earth are A(32.8°N, 26°E) and B(21.2°S, 26°E).
Calculate in kilometres the shortest distance between A and B. (Take the radius of the earth to be 6370 km and π = 22/7) (3 marks)
0 Comments
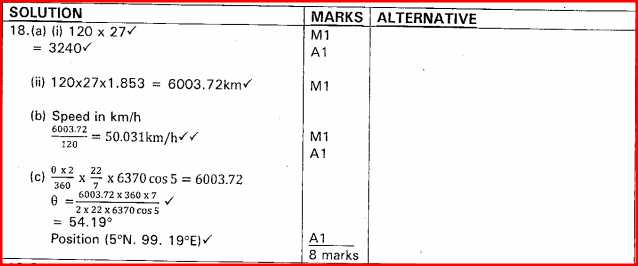
LONGITUDES & LATITUDES | KCSE 1997 | PAPER 1 | SECTION B | FORM 4 LEVELA ship leaves an island (5°N, 45°E) and sails due east for 120 hours to another island. The average speed of the ship is 27 knots.
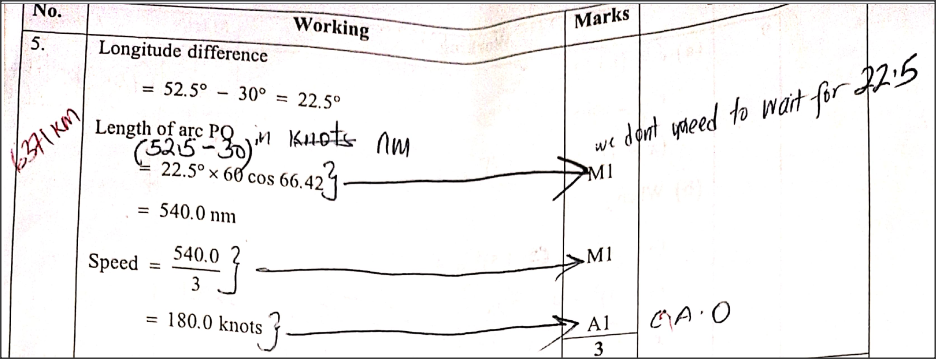
(take 1 nautical mile to be 1.853 Km and the radius of the earth to be 6370 Km) QUESTION 5 | KCSE 2023 | LONGITUDES & LATITUDES | PAPER 2 | FORM 4 LEVELA plane took 3 hours to fly from P(66.42°N, 30°E) to Q(66.42°N, 52.5°E). Determine the speed of the plane in knots correct to one decimal place. (3 marks)
QUESTION 11 | KCSE 2021 | LONGITUDES | PAPER 2 | FORM 4 LEVELA point Q is 2000 nm to the West of a point P(40°N, 155°W). Find the longitude of Q to the nearest degree. (3 marks)
QUESTION 15 | KCSE 2022 | LONGITUDES | PAPER 2 | FORM 4 LEVELAn aircraft took off from an airport A(0°, 40°W) at 1100 h local time. The aircraft landed at airport B(0°, 65°W) at 1200 h local time.
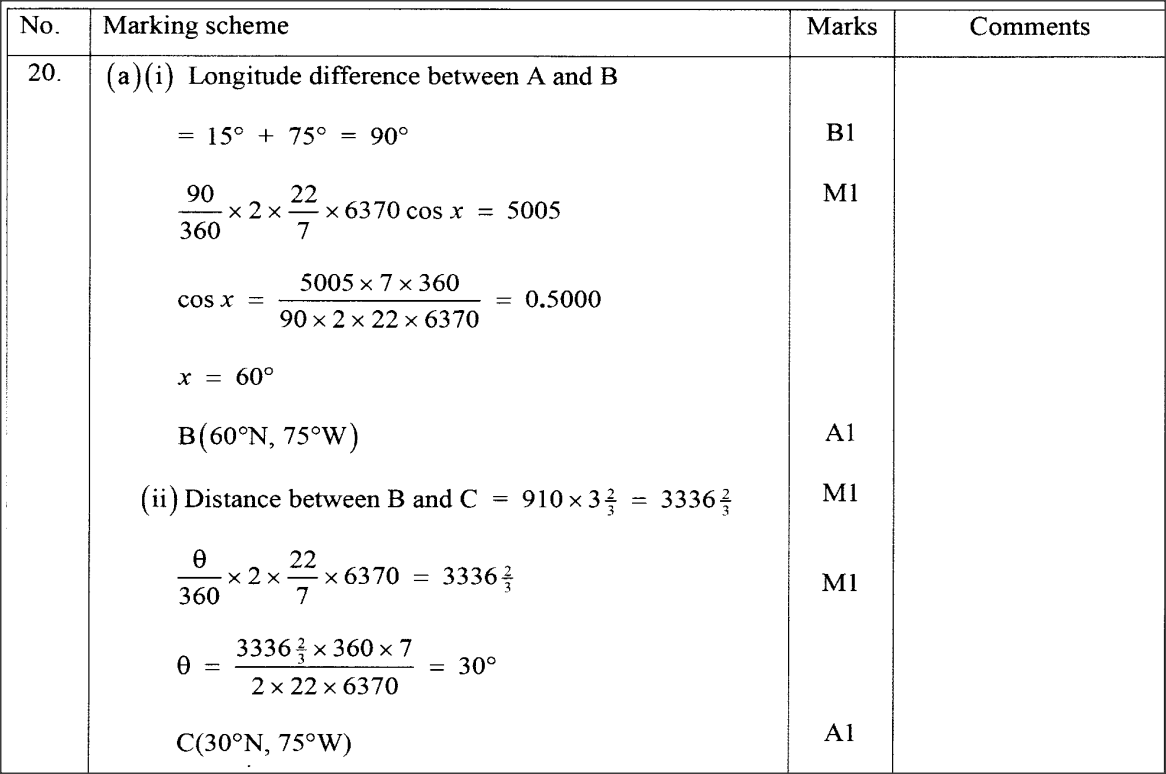
Determine the speed of the aircraft in knots. (4 marks) An aircraft took off from point A (x degrees North, 15 degrees east) at 0720h, local time. It flew due west to another point B (x degrees North, 75 degrees West) a distance of 5005 km from A.KCSE 2020 MATHEMATICS ALT A PAPER 2 QUESTION 20(a) A and B are two points on earth’s surface and on latitude 400 N. The two points are on the longitude 500W and 1300E respectively. Calculate the distance from A to B along a parallel of latitude in kilometers. (2mks)(b) The shortest distance from A to B along a great circle in kilometres (Take p = 22/7 and radius of the earth = 6370km) (2mks)LONGITUDES AND LATITUDES | Distance between two points along the small and great circles in nautical miles and kilometres. | FORM 4 LEVEL | PAPER 2 QUESTIONS | SECTION B(a) (i) Taking the radius of the earth, R= 6370km and π = 22/7, calculate the shortest distance between the two cities P(60oN, 29oW) and Q(60oN, 31oE) along the parallel of latitude. (3mks)(ii) If it is 1200hrs at P, what is the local time at Q. (3mks)(b) An aeroplane flew due south from a point A (60oN, 45oE) to a point B. the distance covered by the aeroplane was 8000km. determine the position of B. (4mks)
Form 4 Mathematics
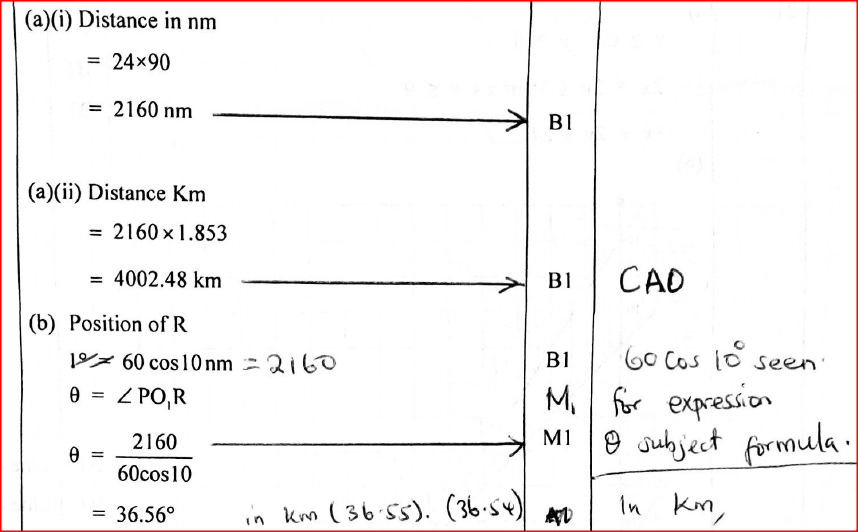
A ship left point P(10°S, 40°E) and sailed due East for 90 hours at an average speed of 24 knots to a point R.(Take 1 nautical mile (nm) to be 1.853 km and radius of the earth to be 6370 km)
(a) Calculate the distance between P and R in: (i) nm; (ii) km. (b) Determine the position of point R. (c) Find the local time, to the nearest minute, at point R when the time at P is 11:00a.m. Form 4 Mathematics
The position of two points C and D on the earth’s surface are (θ°N, l0°E) and (θ°N, 30°E)
respectively. The distance between the two points is 600 nm. Determine the latitude on which C and D lie. Form 4 Mathematics
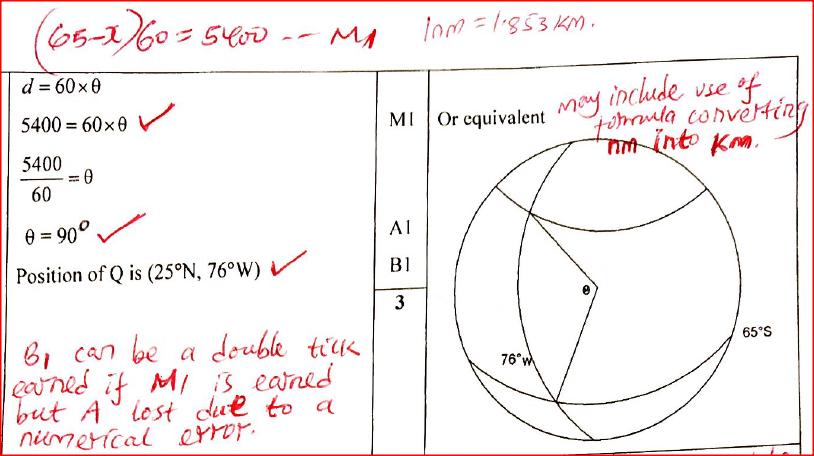
An aircraft took off from a point P (65° S, 76° W) and flew due North to a point Q. The distance between P and Q is 5400 nm.
Determine the position of Q. Form 4 Mathematics
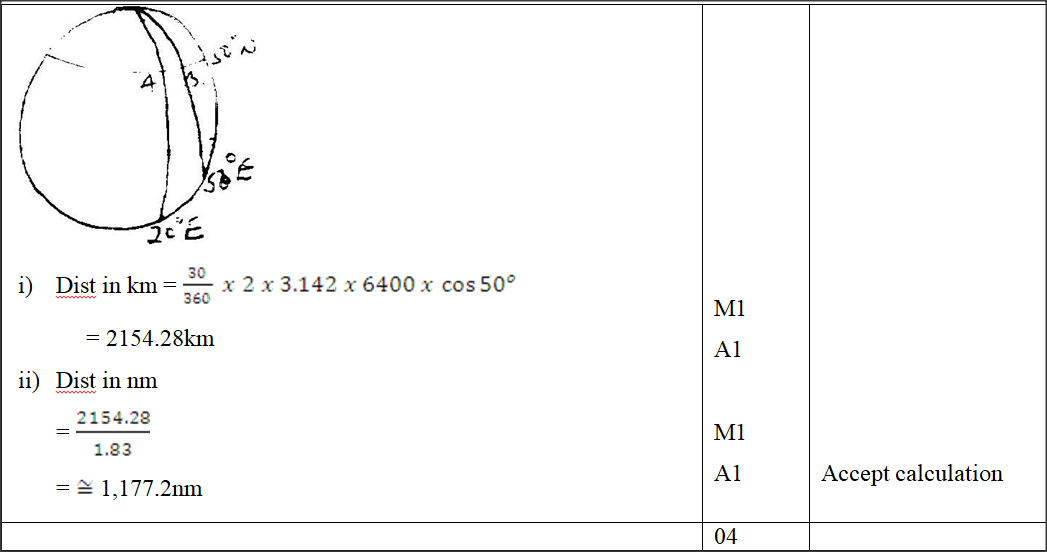
A tourist took 1 hour 20 minutes to travel by an aircraft from town T(3°S, 35°E) to town U(9°N, 35°E, ). (Take the radius of the earth to be 6370km and π = 22/7)
(a) Find the average speed of the aircraft. (a) After staying at town U for 30 minutes, the tourist took a second aircraft to town V(9°N, 5°E), The average speed of the second aircraft was 90% that of the first aircraft Determine the time, to the nearest minute, the aircraft took to travel from U to V. (c) When the journey started at town T, the local time was 0700h. Find the local time at V when the tourist arrived. Form 4 Mathematics
The positions of two points P and Q, on the surface of the earth are P(45 °N, 36°E) and Q(45 °N, 71°E). Calculate the distance, in nautical miles, between P and Q, correct to 1 decimal place.
Form 4 Mathematics
The shortest distance between two points A (40°N, 20°W) and B (0°S, 20°W) on the surface of y the earth is 8008km. Given that the radius of the earth is 6370km,
determine the position of B. (Take n = 22/7 ). Form 4 Mathematics
A ship leaves port p for port R though port Q.Q is 200 km on a bearing of 2200 from P.R is 420 km on the bearing of 1400 from from Q.
Form 4 Mathematics
Two towns A and B lie on the same latitude in the northern hemisphere. When its 8am at A, the time at B is 11.00am.
Form 4 Mathematics
The position of two towns are (20 S,300 E) and 20S, 37.4 0E) calculate , to the nearest km, the shortest distance between the two towns.(take the radius ofthe earth to be 6370 km)
Form 4 Mathematics
A tourist took 1 h 20 minutes to travel by an aircraft from town T(3°S, 35°E) to town U(9°N, 35°E). (Take the radius of the earth to be 6370km and π =22/7
(a) Find the average speed of the aircraft. (b) After staying at town U for 30 minutes, the tourist took a second aircraft to town V(9°N, 5°E). The average speed of the second aircraft was 90% that of the first aircraft. Determine the time, to the nearest minute, the aircraft took to travel from U to V (c) When the journey started at town T, the local time was 0700h. Find the local time at V when the tourist arrived. Form 4 Mathematics
A point M (60°N, 18°E) is on the surface of the earth. Another point N is situated at a distance of 630 nautical miles east of M.
Find: (a) the longitude difference between M and N; (b) The position of N. Form 4 Mathematics
The positions of three ports A, B and C are (34°N, 16°W), (34°N. 24°E) and (26°S, 16°W) respectively.
(a) Find the distance in nautical miles between: (i) Ports A and B to the nearest nautical miles; (ii) Ports A and C. (b) A ship left Port A on Monday at 1330 h and sailed to Port B at 40 knots. Calculate: (i) the local time at Port B when the ship left Port A; (ii) the day and the time the ship arrived at port B. Form 4 Mathematics
Point P (400S, 450E) and point Q (400S, 600W) are on the surface of the Earth.
Calculate the shortest distance along a circle of latitude between the two points. Form 4 Mathematics
An aero plane flies at an average speed of 500 knots due East from a point p (53.40e) to another point Q. It takes 2 ¼ hours to reach point Q. Calculate:
(i) The distance in nautical miles it traveled; (ii) The longitude of point Q to 2 decimal places Form 4 Mathematics
Two places A and B are on the same circle of latitude north of the equator. The longitude of A is 1180W and the longitude of B is 1330E. The shorter distance between A and B measured along the circle of latitude is 5422 nautical miles.Find, to the nearest degree, the latitude on which A and B lie
|
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|










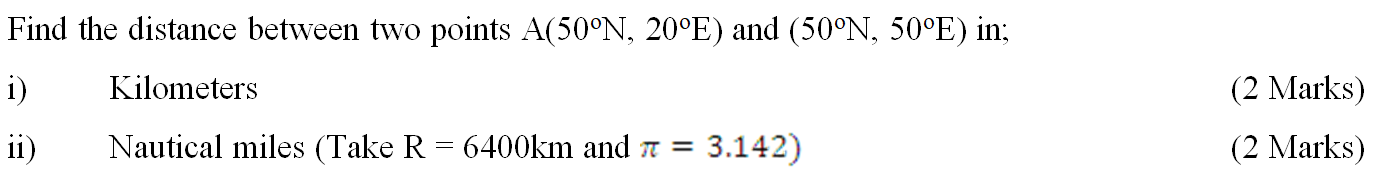


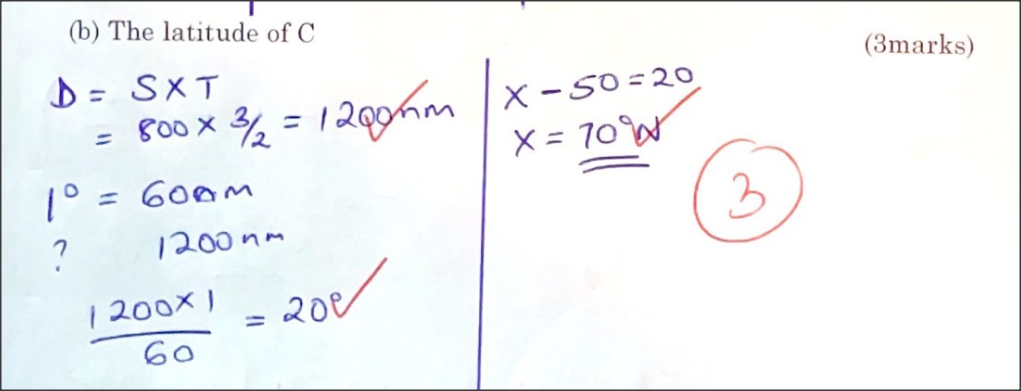










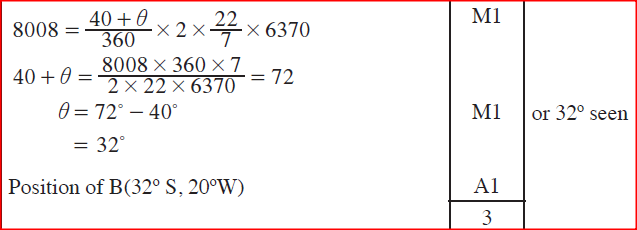





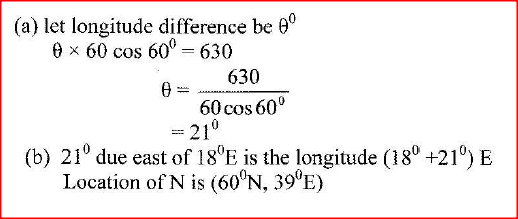






 RSS Feed
RSS Feed