KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
Form 3 Mathematics
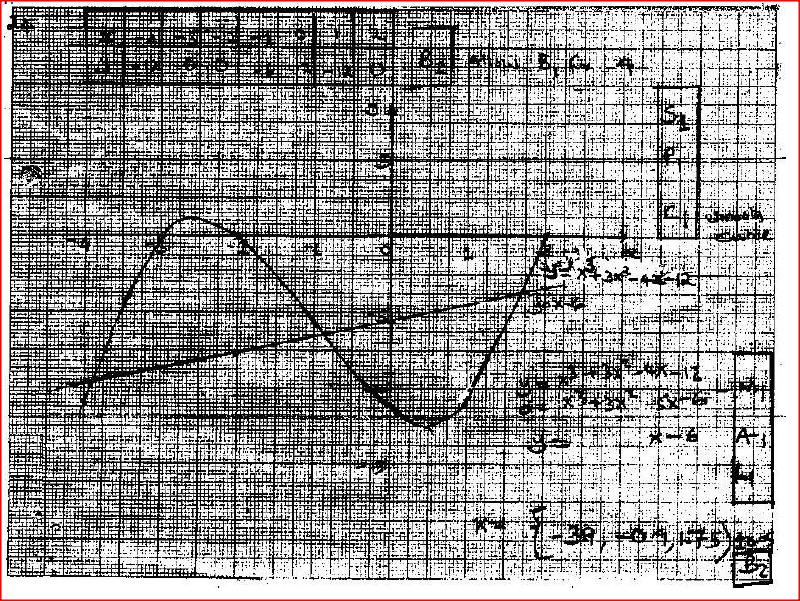
The table below shows values of x and some values of y for the curvey = x +3+3x2+-4x-12 in the range -4 ≤ x ≤ 2.
a) Complete the table by filling in the missing values of y.
b) On the grid provided, draw the graph y=x3 + 3x2+ -4x – 12 for -4 ≤ x ≤ 2.Use the scale. Horizontal axis 2cm for I unit and vertical axis 2cm for 5 units.
c) By drawing a suitable straight line on the same grid as the curve, solve the equation x3+3x2-5x-6=0
0 Comments
Form 1 Mathematics
Halima deposited Ksh. 109375 in a financial institution which paid simple interest at the rate of 8% p.a. At the end of 2 years, she withdrew all the money. She then invested the money in share. The value of the shares depreciated at 4% p.a. during the first year of investment. In the next 3 years, the value of the shares appreciated at the rate of 6% every four months
a) Calculate the amount Halima invested in shares. b) Calculate the value of Halima's shares. (i) At the end of the first year; (ii) At the end of the fourth year, to the nearest shilling. c) Calculate Halima„s gain from the share as a percentage. (ii) Find the values of x and y. (iii) Calculate the time taken before the policemen were unable to communicate. Form 4 MathematicsForm 2 Mathematics
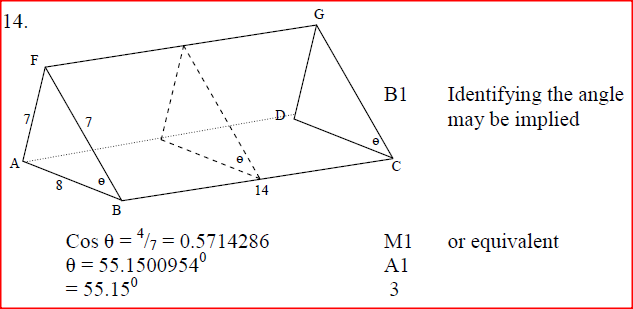
Two policemen were together at a road junction. Each had a walkie talkie. The maximum distance at which one could communicate with the other was 2.5 km.
One of the policemen walked due East at 3.2 km/h while the other walked due North at 2.4 km/h the policeman who headed East traveled for x km while the one who headed North traveled for y km before they were unable to communicate. (a) Draw a sketch to represent the relative positions of the policemen. (b) (i) From the information above form two simultaneous equations in x and y. Form 2 MathematicsForm 4 Mathematics
a) complete the table below, giving the values correct to 2 decimal places.
b) On the grid provided, draw the graphs of y=sin 2x and y=3cosx-2 for 00 ≤ x ≤3600 on the same axes.
Use a scale of 1 cm to represent 300 on the x-axis and 2cm to represent 1 unit on the y-axis. c) Use the graph in (b) above to solve the equation 3 Cos x – sin 2x = 2. d) State the amplitude of y=3cosx-2. Form 1 Mathematics
a) A trader deals in two types of rice; type A and with 50 bags of type B. If
he sells the mixture at a profit of 20%, calculate the selling price of one bag of the mixture. b) The trader now mixes type A with type B in the ratio x: y respectively. If the cost of the mixture is Ksh 383.50 per bag, find the ratio x: y. c) The trader mixes one bag of the mixture in part (a) with one bag of the mixture in part (b). Calculate the ratio of type A rice to type B rice in this mixture. Form 4 Mathematics
Find in radians, the values of x in the interval 00≤ x ≤ 2π0+ for which 2 cos 2x=1.
(Leave the answers in terms of π ) Form 4 Mathematics
A particle moves in a straight line from a fixed point. Its velocity Vms-1 after t seconds is given by V=9t2 – 4t +1
Calculate the distance traveled by the particle during the third second. Form 4 MathematicsForm 3 Mathematics
The equation of a circle is given by 4x2 + 4y2+- 8x+ 20y – 7 = 0. Determine the coordinates of the centre of the circle.
Form 4 Mathematics
Points A(2,2)and B(4,3) are mapped onto A‟(2,8) and b‟ (4,15) respectively by a transformation T.
Find the matrix of T. Form 2 MathematicsForm 4 Mathematics
An aero plane flies at an average speed of 500 knots due East from a point p (53.40e) to another point Q. It takes 2 ¼ hours to reach point Q. Calculate:
(i) The distance in nautical miles it traveled; (ii) The longitude of point Q to 2 decimal places Form 3 Mathematics
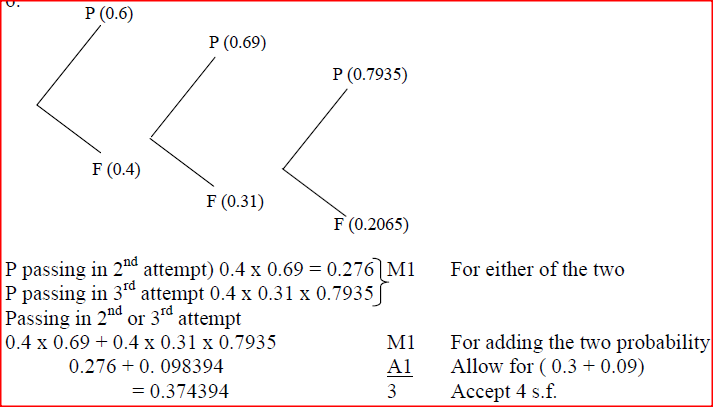
A student at a certain college has a 60% chance of passing an examination at the first attempt. Each time a student fails and repeats the examination his chances of passing are increased by 15%
Calculate the probability that a student in the college passes an examination at the second or at the third attempt. Form 3 Mathematics
The top of a table is a regular hexagon. Each side of the hexagon measures 50.0 cm. Find the maximum percentage error in calculating the perimeter of the top of the table.
Form 3 MathematicsForm 1 MathematicsForm 2 MathematicsForm 4 Mathematics
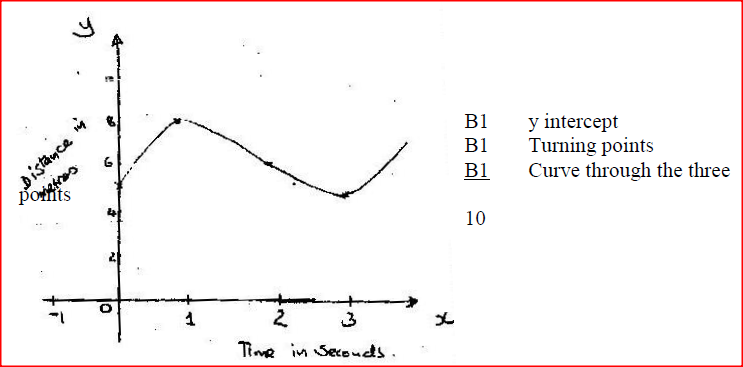
The distance s metres from a fixed point O, covered by a particle after t seconds is given by the equation;
S =t3 -6t2 + 9t + 5. a) Calculate the gradient to the curve at t=0.5 seconds b) Determine the values of s at the maximum and minimum turning points of the curve. c) On the space provided, sketch the curve of s= t3-6t2+9t + 5. Form 3 Mathematics
A group of people planned to contribute equally towards a water project which needed Ksh 200 000 to complete, However, 40 members of the group without from the project.
As a result, each of the remaining members were to contribute Ksh 2500. a) Find the original number of members in the group. b) Forty five percent of the value of the project was funded by Constituency Development Fund (CDF). Calculate the amount of contribution that would be made by each of the remaining members of the group. c) Member‟s contributions were in terms of labour provided and money contributed. If the ratio of the value of labour to the money contributed was 6:19; calculate the total amount of money contributed by the members. Form 2 Mathematics
The diagram below represents a conical vessel which stands vertically. The which stands vertically,. The vessels contains water to a depth of 30cm. The radius of the surface in the vessel is 21cm. (Take π=22/7).
a) Calculate the volume of the water in the vessels in cm3
b) When a metal sphere is completely submerged in the water, the level of the water in the vessels rises by 6cm. Calculate: (i) The radius of the new water surface in the vessel; (ii) The volume of the metal sphere in cm3 (iii) The radius of the sphere. |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|
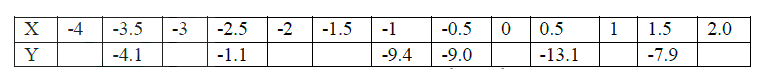







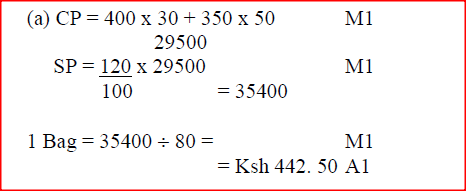













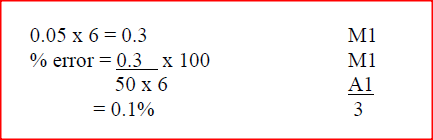
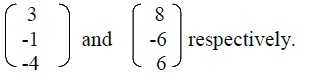

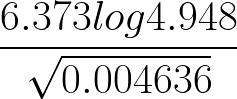

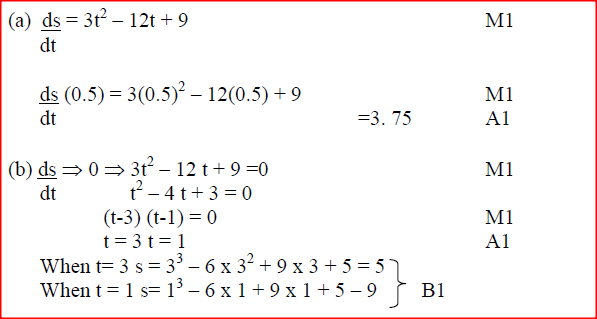





 RSS Feed
RSS Feed