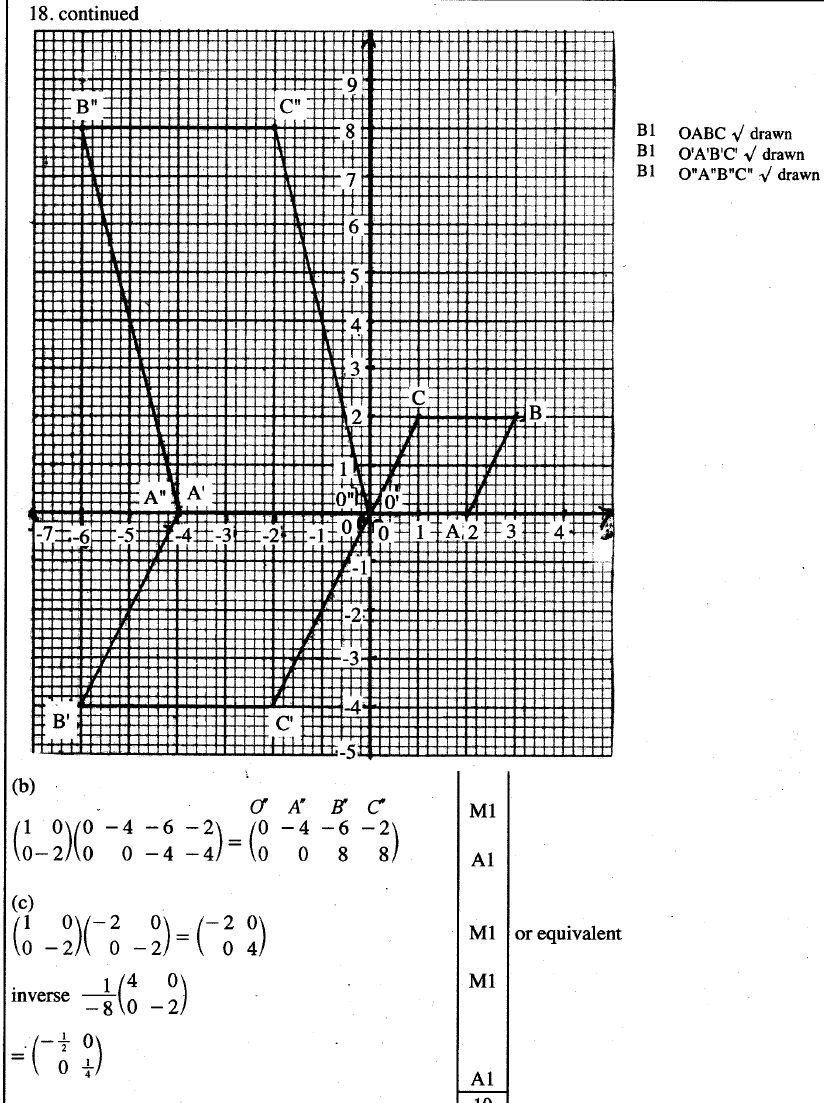
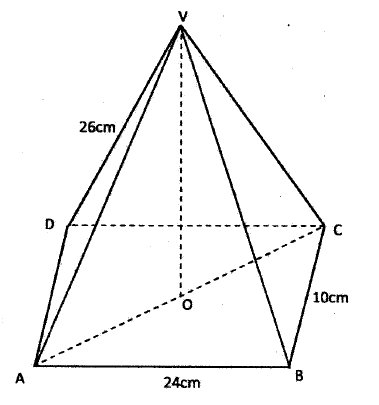
KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
Form 4 Mathematics
The acceleration of a body moving along a straight line is (4 - t) m/s2 and its velocity is v m/s after t seconds.
(a) (i) If the initial velocity of the body is 3 m/s, express the velocity v in terms of t. (ii) Find the velocity of the body after 2 seconds. (b) Calculate: (i) the time taken to attain maximum velocity; (ii) the distance covered by the body to attain the maximum velocity.
0 Comments
Form 3 Mathematics
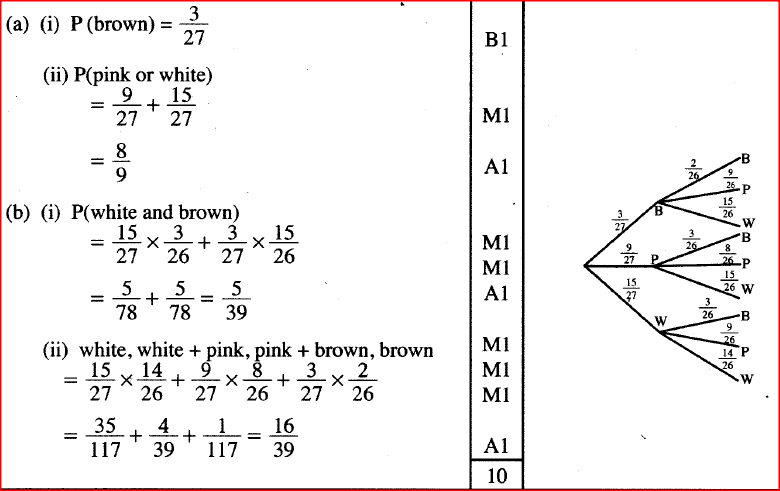
A box contains 3 brown, 9 pink and 15 white clothes pegs. The pegs are identical except for the colour.
(a) Find the probability of picking: (i) a brown peg; (ii) a pink or a white peg. (b) Two pegs are picked at random, one at a time, without replacement. Find the probability that: (i) a white peg and a brown peg are picked; (ii) both pegs are of the same colour. Form 4 Mathematics
A tourist took 1 h 20 minutes to travel by an aircraft from town T(3°S, 35°E) to town U(9°N, 35°E). (Take the radius of the earth to be 6370km and π =22/7
(a) Find the average speed of the aircraft. (b) After staying at town U for 30 minutes, the tourist took a second aircraft to town V(9°N, 5°E). The average speed of the second aircraft was 90% that of the first aircraft. Determine the time, to the nearest minute, the aircraft took to travel from U to V (c) When the journey started at town T, the local time was 0700h. Find the local time at V when the tourist arrived. Form 1 Mathematics
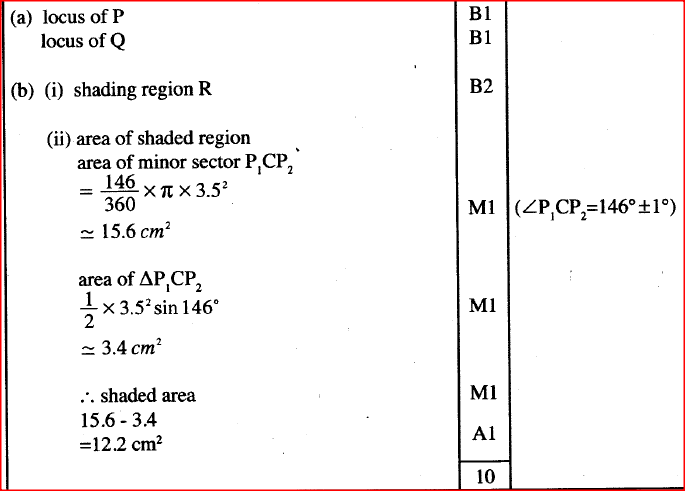
(a) on the same diagram construct:
(i) triangle ABC such that AB = 9 cm, AC= 7 cm and angle CAB = 60°; (ii) the locus of a point P such that P is equidistant from A and B; (iii) the locus of a point Q such that CQ ≤ 3.5cm. (b) On the diagram in part (a): (i) shade the region R, containing all the points enclosed by the locus of P and the locus of Q, such that AP ≥ BP; (ii) find the area of the region shaded in part (b)(i) above. Form 3 Mathematics
In June of a certain year, an employee's basic salary was Ksh 17000. The employee was also paid a house allowance of Ksh 6000, a commuter allowance
of Ksh 2500 and a medical allowance of Ksh 1 800. In July of that year, the employee's basic salary was raised by 2%. (a) Calculate the employees: (i) basic salary for July; (ii) total taxable income in July of that year. (b) In that year, the Income Tax Rates were as shown in the table below:
Given that the Monthly Personal Relief was Ksh 1056, calculate the net tax paid by the employee.
Form 3 Mathematics
In triangle OPQ below, OP = p, OQ = q. Point M lies on OP such that OM : MP = 2 : 3 and point N lies on OQ such that ON : NQ = 5:1. Line PN
intersects line MQ at X.
(a) Express in terms of p and q:
(i) PM (ii) QM. (c) Given that PX = kPN and QX = rQM, where k and r are scalars: (i) write two different expressions for OX in terms of p, q, k and r; (ii) find the values of k and r; (iii) determine the ratio in which X divides line MQ. Form 4 MathematicsForm 1 Mathematics
Amaya was paid an initial salary of Ksh 180 000 per annum with a fixed annual increment. Bundi was paid an initial salary of Ksh 150000 per annum with a
10% increment compounded annually. (a) Given that Amaya's annual salary in the 11th year was Ksh 288 000, determine: (i) his annual increment; (ii) the total amount of money Amaya earned during the 11 years. (b) Determine Bundi's monthly earnings, correct to the nearest shilling, during the eleventh year. (c) Determine, correct to the nearest shilling: (i) the total amount of money Bundi earned during the 11 years. Form 4 MathematicsForm 3 MathematicsForm 4 MathematicsForm 3 Mathematics
(a) Expand (1 + x)7 up to the 4th term.
(b) Use the expansion in part (a) above to find the approximate value of (0.94)7 Form 3 Mathematics
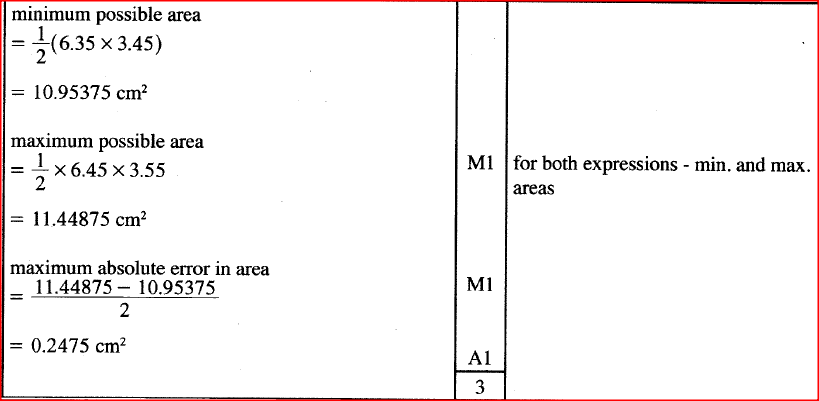
The base and height of a right angled triangle were measured as 6.4cm and 3.5 cm respectively. Calculate the maximum absolute error in the area of the triangle.
Form 2 Mathematics
The masses in kilograms of 20 bags of maize were;
90, 94, 96, 98, 99, 102, 105, 91, 102, 99, 105, 94, 99, 90, 94, 99, 98, 96, 102 and 105. Using an assumed mean of 96kg, calculate the mean mass, per bag, of the maize. Form 1 Mathematics
Kago deposited Ksh 30 000 in a financial institution that paid simple interest at the rate of 12% per annum. Nekesa deposited the same amount of money
as Kago in another financial institution that paid compound interest. After 5 years, they had equal amounts of money in the financial institutions. Determine the compound interest rate per annum, to 1 decimal place, for Nekesa's deposit. Form 1 Mathematics
Construct a circle centre x and radius 2.5 cm. Construct a tangent from a point P, 6 cm from x to touch the circle at R. Measure the length PR.
Form 2 Mathematics
Given that P = 2i- 3j + k, Q = 3i – 4j- 3k and R = 3P + 2 Q, find the magnitude of R to 2 significant figures.
Form 1 Mathematics
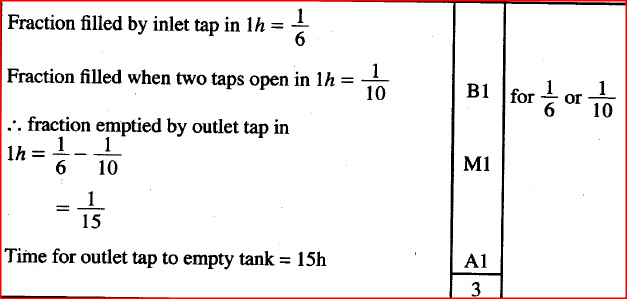
An inlet tap can fill an empty tank in 6 hours. It takes 10 hours to fill the tan kwhen the inlet tap and an outlet tap are both opened at the same time. Calculate
the time the outlet tap takes to empty the full tank when the inlet tap is closed. Form 2 Mathematics
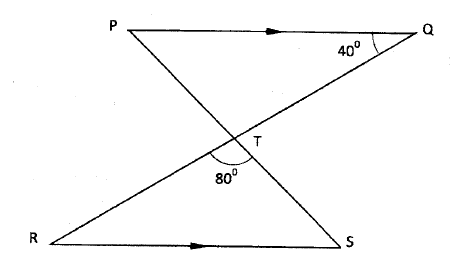
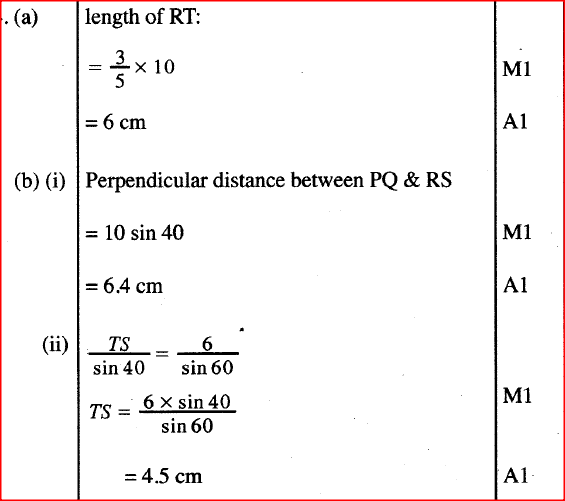
In the figure below, PQ is parallel to RS. The lines PS and RQ intersect at T. RQ = 10 cm, RT:TQ = 3:2, angle PQT = 40° and angle RTS - 80°.
(a) Find the length of RT.
(b) Determine, correct to 2 significant figures: (i) the perpendicular distance between PQ and RS; (ii) the length of TS. (c) Using the cosine rule, find the length of RS correct to 2 significant figures. (d) Calculate, correct to one decimal place, the area of triangle RST. Form 1 Mathematics
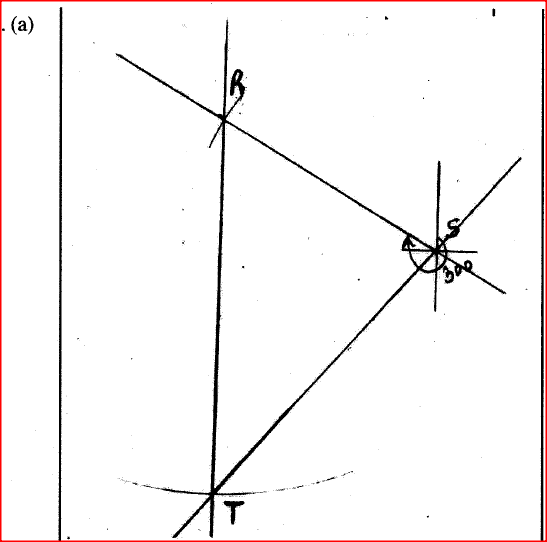
Three pegs R, S and T are on the vertices of a triangular plain field. R is 300 m from S on a bearing of 300° and T is 450 m directly south of R.
(a) Using a scale of 1 cm to represent 60 m, draw a diagram to show the positions of the pegs. (b) Use the scale drawing to determine: (i) the distance between T and S in metres: (ii) the bearing of T from S. (c) Find the area of the field, in hectares, correct to one decimal place. Form 4 Mathematics
The equation of a curve is y = 2x3 + 3x2.
(a) Find: (i) the x - intercept of the curve; (ii) the y - intercept of the curve. (b) (i) Determine the stationery points of the curve. (ii) For each point in (b) (i) above, determine whether it is a maximum or a minimum. (c) Sketch the curve. |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|

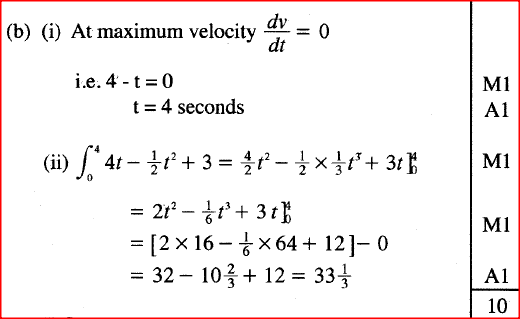






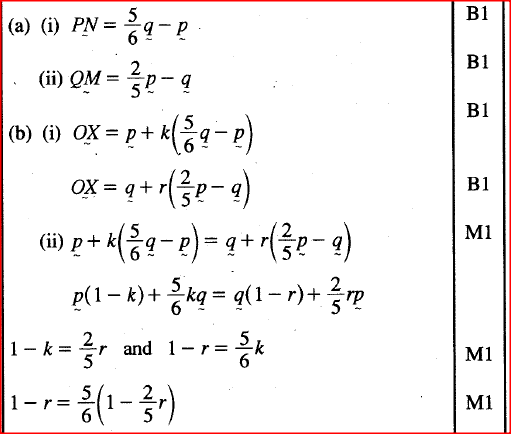

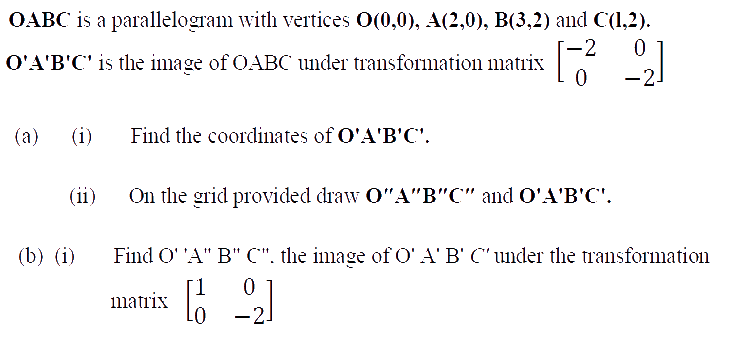
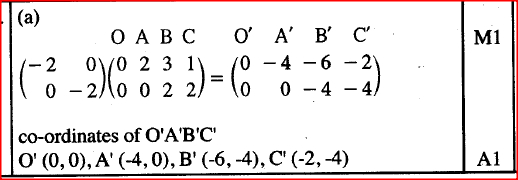








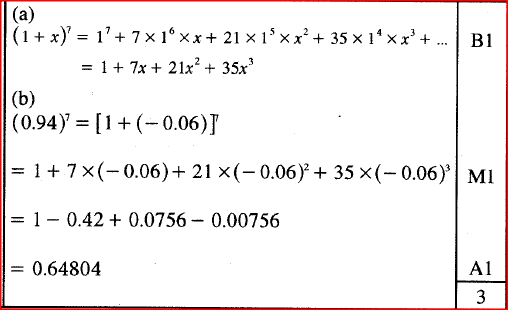






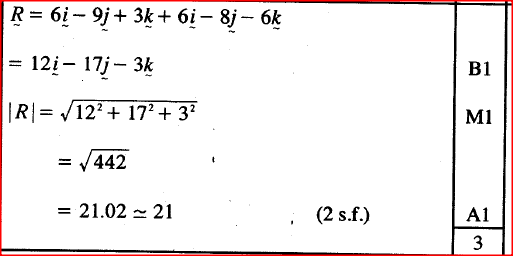







 RSS Feed
RSS Feed