KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
| LINEAR INEQUALITIES | FORM 2 LEVEL | SECTION I | PAPER 1 | ALT B | KCSE 2011 | QUESTION 6 |Find the integral values of x which satisfy the inequality 3x ≤ 2x + 3 < 4x + 5. (3 marks)
0 Comments
ALT B | LINEAR INEQUALITIES | SECTION 1 | QUESTION 10 | KCSE 2010 | FORM 2 LEVELSolve the inequality 3x - 2 < 10 + x ≤ 2 + 5x. (3 marks)
QUESTION 4 | KCSE 2021 | LINEAR Inequalities | PAPER 1 | FORM 2 LEVELSolve [5/3] - 2x < 1- [2/3]x <= 2 - x. Hence list the integral values that satisfy the 3 -2x<1-x2-x. 3 inequalities. (3 marks)
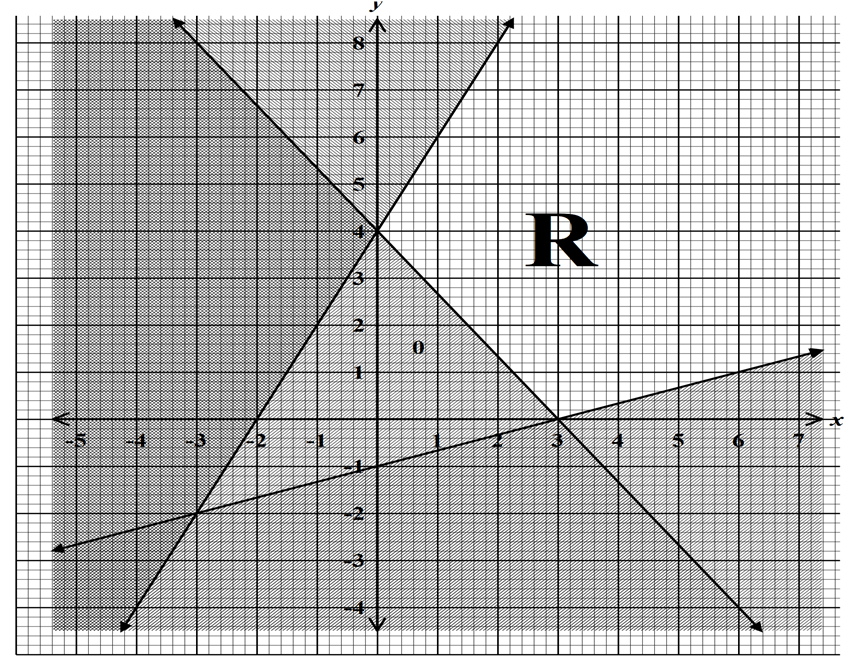
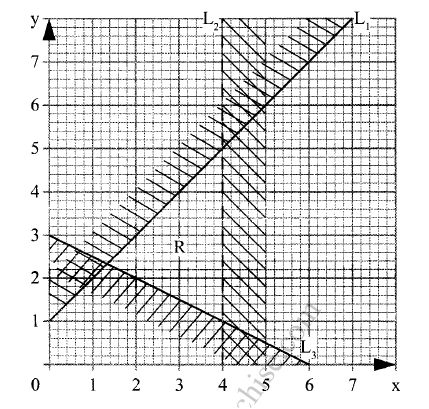
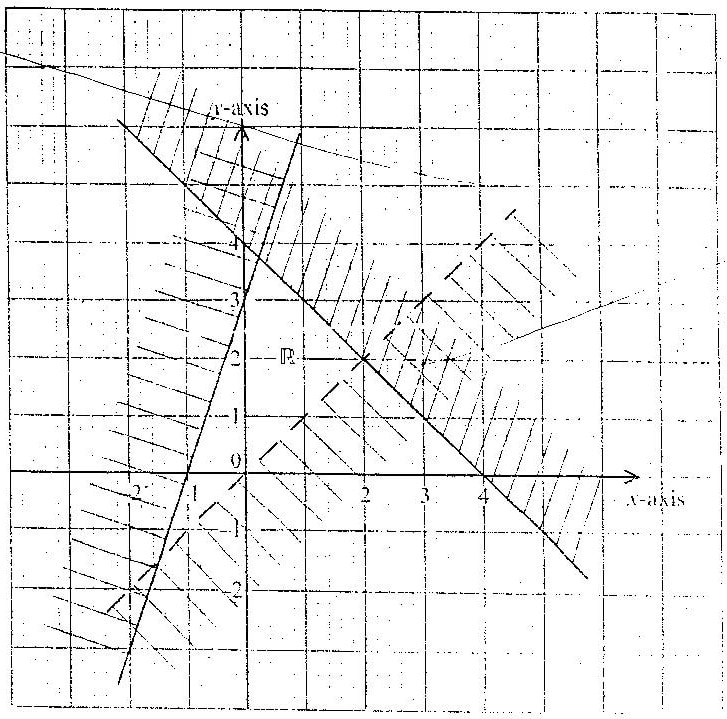
The height of tree seedlings in a nursery were measured and recorded as in the table below11/5/2023 The height of tree seedlings in a nursery were measured and recorded as in the table belowThe unshaded region in the figure below is reflected in the x-axis. Write down the inequalities which satisfy the new region. (3mks)Given that 1.5 ≤ x ≤ 3.8 and 2.4 ≤ y ≤ 5, determine the smallest and the greatest value of x – y and hence the range of x – y. (3 Marks) ANSWERState the inequalities that satisfy the region defined by R. (3marks)Form 4 Mathematics
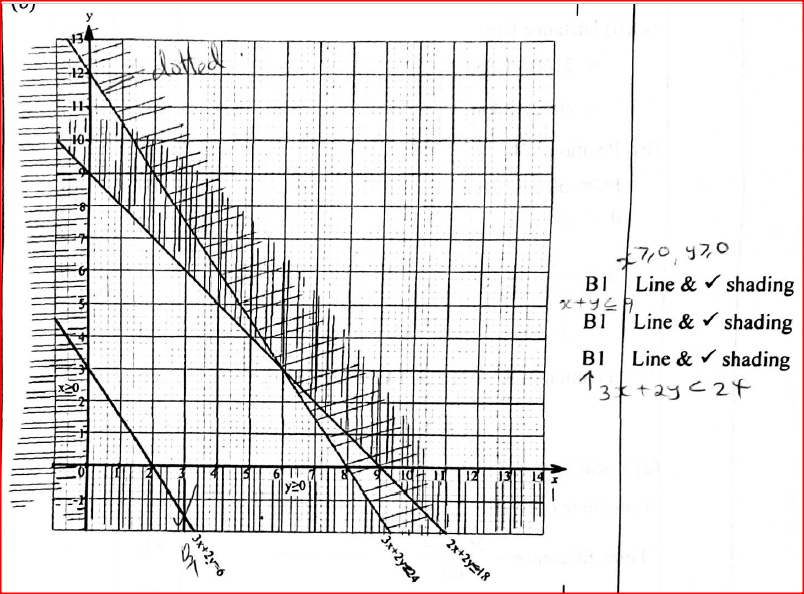
A workshop makes cupboards and tables using two artisans A and B every cupboard made requires 3 days of work by artisan A and 2 days of work by artisan B. Every table made requires 2 days of work by artisan A and 2 days of work by artisan B.
In one month artisan A worked in less than 24 while artisan B Worked for Not More Than 18 Days. The workshop made x cupboards and y tables in that month. (a) Write all the inequalities which must be satisfied by x and y. (b) Represent the inequalities in (a) on the grid provided. (c) The workshop makes a profit of Ksh 6 000 on each cupboard and Ksh4 000 on each table. Find the number of cupboards and the number of tables that must be made for maximum profit and hence determine the maximum profit. Form 2 Mathematics
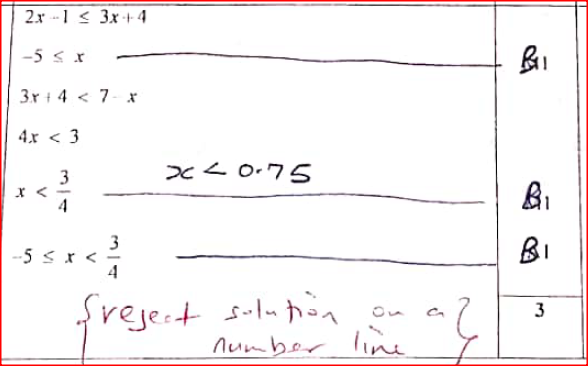
Solve the inequality 2x - 1 ≤ 3x + 4 < 7 - x.
Related Questions and Answers on Linear InequalitiesForm 4 Mathematics
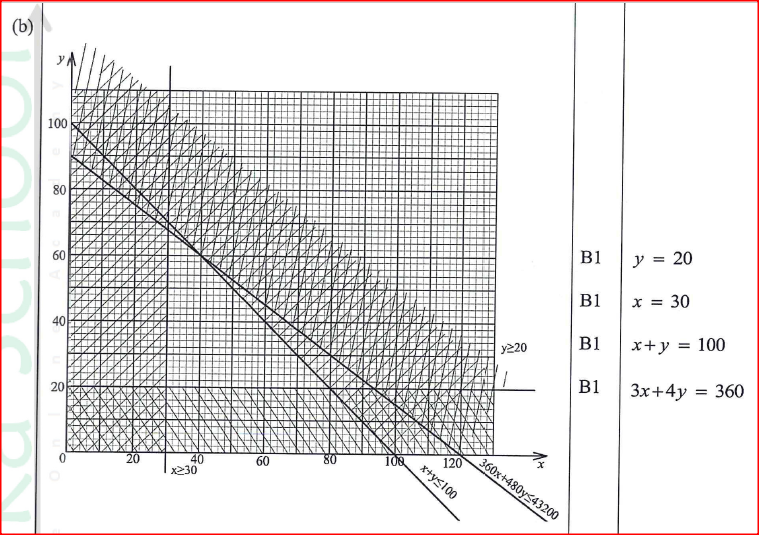
A hotel buys beef and mutton daily. The amount of beef bought must be at least 30kg and that of mutton at least 20 kg. The total mass of beef and mutton bought should not exceed 100 kg. The beef is bought at Ksh 360 per kg and the mutton at Ksh 480 per kg.
The amount of money spent on both beef and mutton should not exceed Ksh 43 200 per day. Let x represent the number of kilograms of beef and y the number of kilograms of mutton. (a) Write the inequalities that represent the above information. (b) On the grid provided, draw the inequalities in (a) above. (c) The hotel makes a profit of ksh 50 on each kg of beef and ksh 60 on each kg of mutton. Determine the maximum profit the hotel can make Form 4 Mathematics
A trader stocks two brands of rice A and B. The rice is packed in packets of the same size. The trader intends to order fresh supplies but his store can accommodate a maximum of 500 packets. He orders at least twice as many packets of A as of B.
He requires at least 50 packets of B and more than 250 packets of A. If he orders x packets of A and y packets of B, (a) Write the inequalities in terms of x and y which satisfy the above information. (b) On the grid provided represent the inequalities in part (a) above (c) The trader makes a profit of Ksh 12 on a packet of type A rice and Ksh 8 on a packet of type B rice. Determine the maximum profit the trader can make. Form 2 MathematicsForm 2 Mathematics
A school decided to buy at least 32 bags of maize and beans. The number of bags of beans were Lo be at least 6. A bag of maize costs Ksh 2500 and a bag of beans costs Ksh 3 500, The school had Ksh 100 000 to purchase the maize and beans. Write down all the inequalities that satisfy the above information,
Form 2 Mathematics
A school decided to buy at least 32 bags of maize and beans. The number of bags of maize were to be more than 20 and the number of bags of beans were to
be at least 6. A bag of maize costs Ksh 2500 and a bag of beans costs Ksh 3500. The school had Ksh 100 000 to purchase the maize and beans. Write down all the inequalities that satisfy the above information.
left
The dimensions of a rectangular floor of a proposed building are such that!
• the length is greater than the width but at most twice the width; • the sum of the width and the length is, more than 8 metres but less than 20 metres. If'x represents the width and y the length. (a) write inequalities to represent the above information. (b) (i) Represent the inequalities in part (a) above on the grid provided. (ii) Using the integral values of x and y, find the maximum possible area of the floor. Form 2 Mathematics
Solve 4 ≤ 3x – 2 ˂ 9 + x hence list the integral value that satisfies the inequality.
Form 2 Mathematics
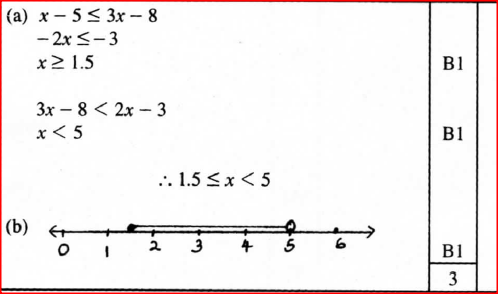
Given the inequalities x – 5 ≤ 3 x – 8 < 2 x – 3.
a) Solve the inequalities; b) Represent the solution on a number line. Form 2 Mathematics
(a) Solve the inequalities 2x — 5 > - 11 and 3 + 2x ≤ 13, giving the answer as a combined inequality.
(b) List the integral values of x that satisfy the combined inequality in (a) above. Form 4 Mathematics
A carpenter takes 4 hours to make a stool and 6 hours to make a chair. It takes the carpenter and at least 144 hours to make x stools and y chairs. The labour cost of making a stool is Ksh 100 and that of a chair is Ksh 200. The total labour cost should not exceed Ksh 4 800. The carpenter must make at least 16 stools and more than 10 chairs.
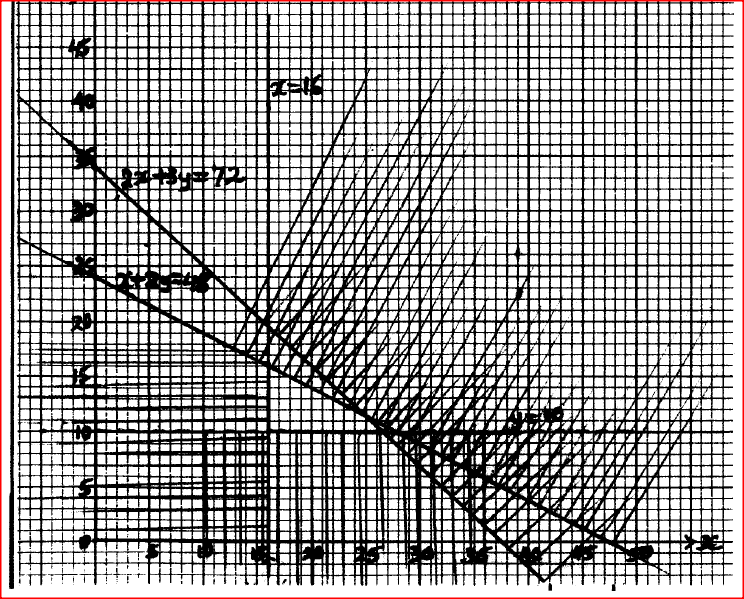
(a) Write down inequalities to represent the above information. (b) Draw the inequalities in (a) above on the grid provided.
(c) The carpenter makes a profit of Ksh 40 on a stool and Ksh loo on a chair.
Use the graph to determine the maximum profi.t the carpenter can make. Form 2 Mathematics
Solve the following inequalities and represent the solutions on a single number line:
3 – 2x < 5 4 – 3x ≥ -8 Form 4 Mathematics
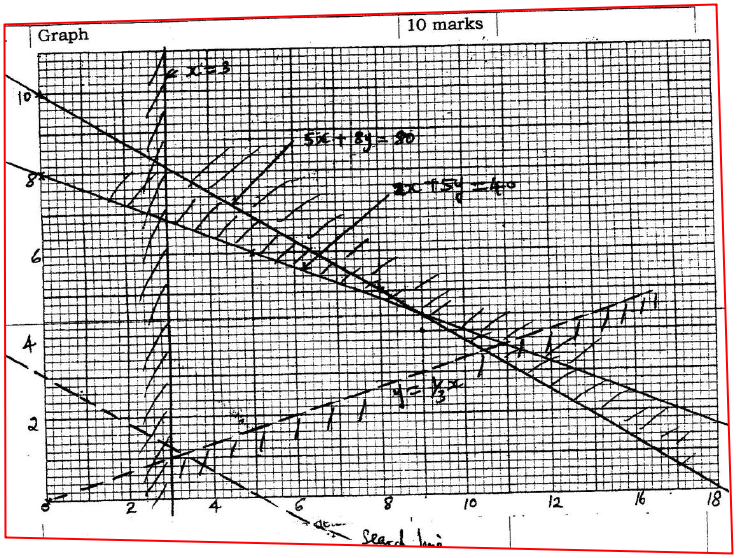
A company is considering installing two types of machines. A and B. The information about each type of machine is given in the table below.
The company decided to install x machines of types A and y machines of type B(a) Write down the inequalities that express the following conditions
I. The number of operators available is 40 II. The floor space available is 80m2 III. The company is to install not less than 3 type of A machine IV. The number of type B machines must be more than one third the number of type A machines (b) On the grid provided, draw the inequalities in part ( a) above and shade the unwanted region (c) Draw a search line and use it to determine the number of machines of each type that should be installed to maximize the daily profit. |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|


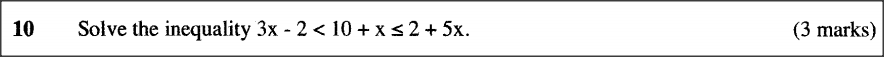










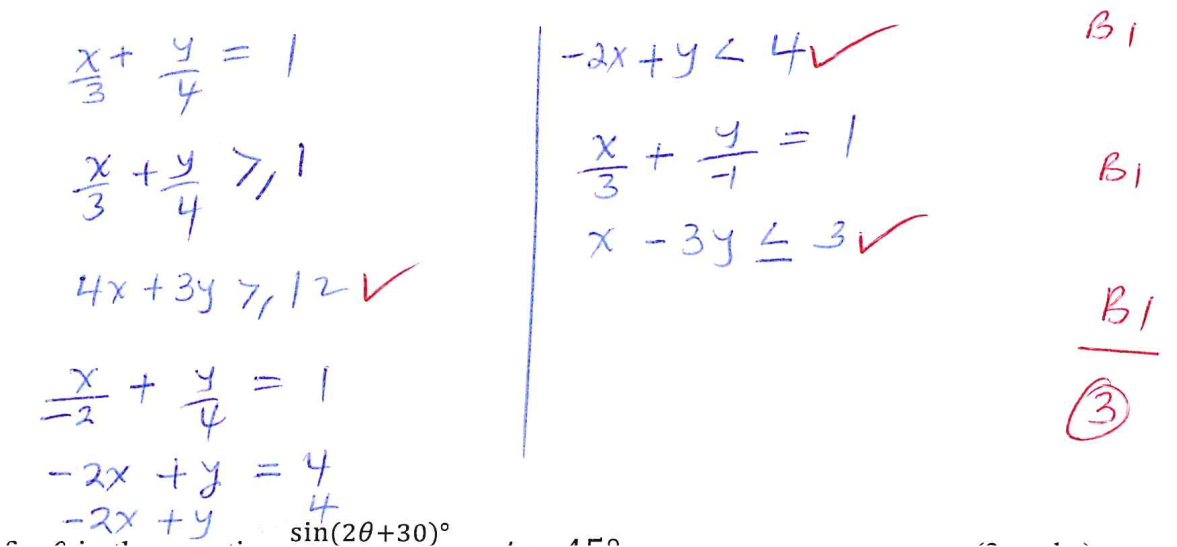
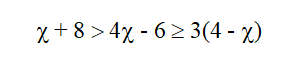



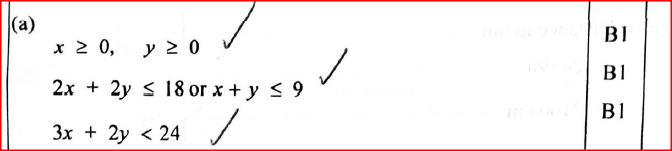
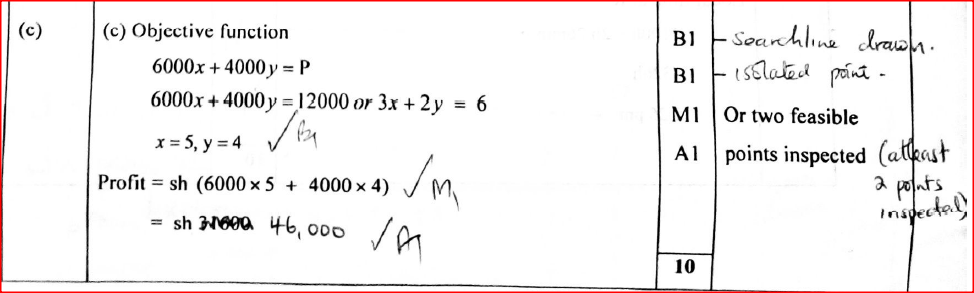
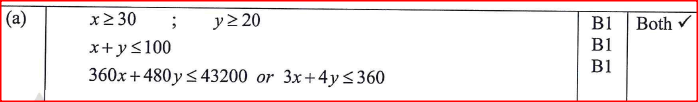
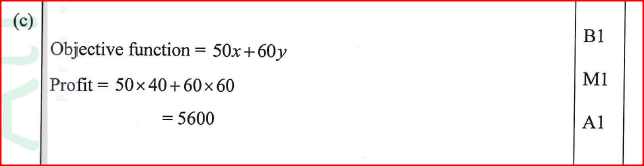











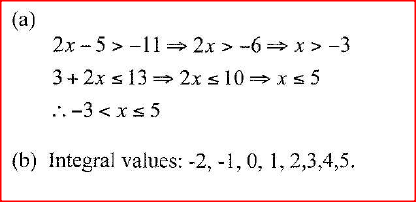

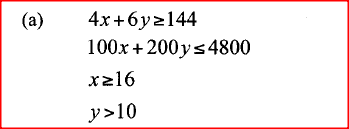

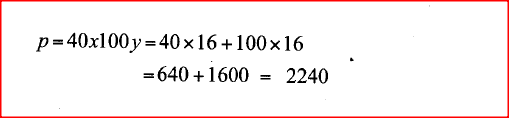

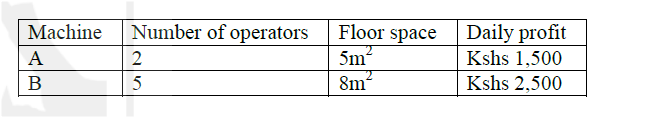

 RSS Feed
RSS Feed