KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
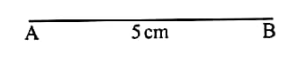
QUESTION 24 | KCSE 2022 | LOCI | PAPER 2 | FORM 4 LEVEL In this question use a ruler and a pair of compasses. The line AB drawn below is a side of triangle ABC in LABC which = 90° and BAC = 60°.
0 Comments
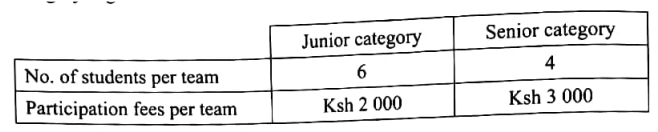
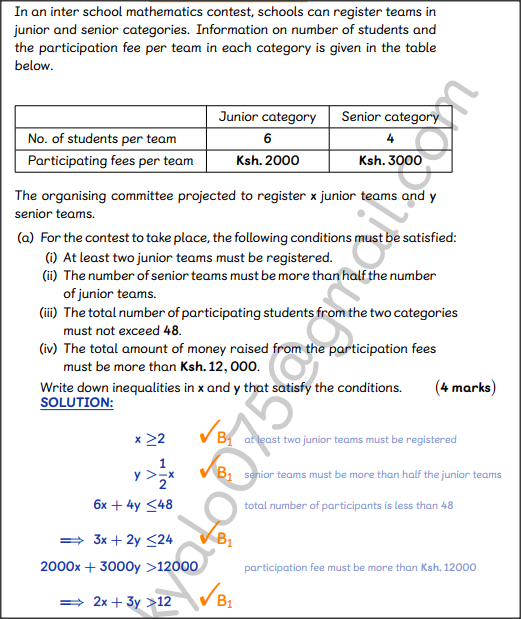
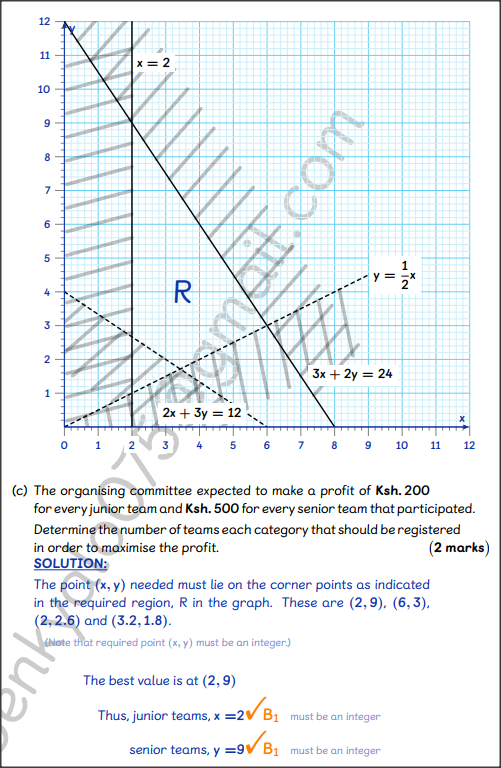
In an inter school mathematics contest, schools can register teams in junior and senior categories.23/12/2023 QUESTION 23 | KCSE 2022 | LINEAR PROGRAMMING | PAPER 2 | FORM 4 LEVELIn an inter school mathematics contest, schools can register teams in junior and senior categories. Information on number of students and the participation fee per team in each category is given in the table below. The organising committee projected to register x junior teams and y senior teams.
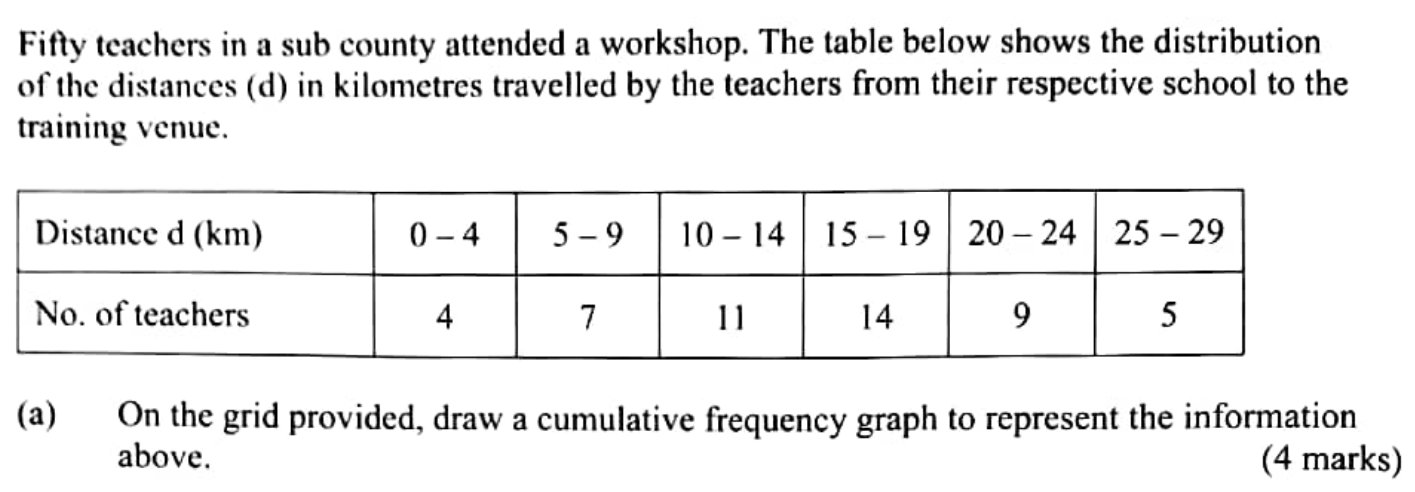
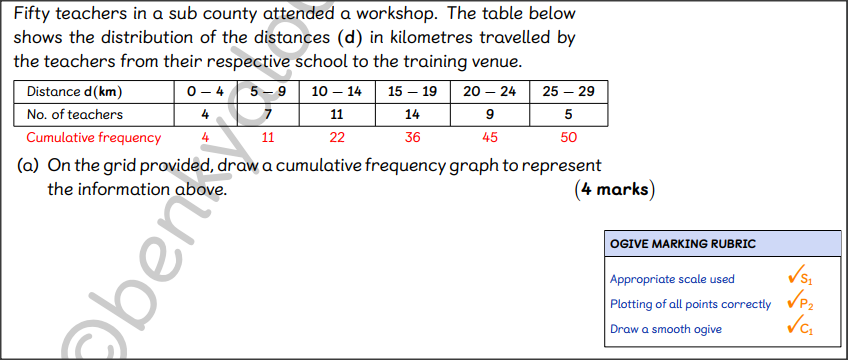
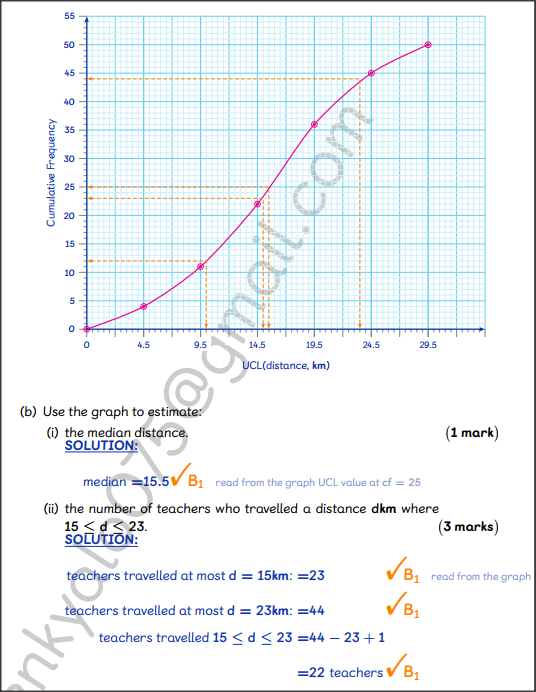
QUESTION 22 | KCSE 2022 | STATISTICS II | PAPER 2 | FORM 4 LEVELFifty teachers in a sub county attended a workshop. The table below shows the distribution of the distances (d) in kilometres travelled by the teachers from their respective school to the training venue.
QUESTION 21 | KCSE 2022 | COMMERCIAL ARITHMETIC II | PAPER 2 | FORM 3 LEVEL(a) Juma bought a house 4 years ago for Ksh 2500000. The value of the house rose steadily over 4 years to its current value of Ksh 3 700000. Calculate, correct to 2 decimal places, the annual rate of appreciation in the value of the house. (3 marks) (b) At the time Juma bought the house in 21(a), Tony also bought a car valued at Ksh 5 100000. The value of the car depreciated steadily at a rate of 2% every 4 months. Determine correct to the nearest shilling, the current value of the car. (3 marks) (c) The house bought in 21(a) continued to appreciate in value at the same rate while the car bought in 21(b) continued to depreciate in value at the same rate. Determine the number of years from the time of purchase, it would take for the value of the house and that of the car to be equal. Give the answer correct to 1 decimal place. (4 marks)
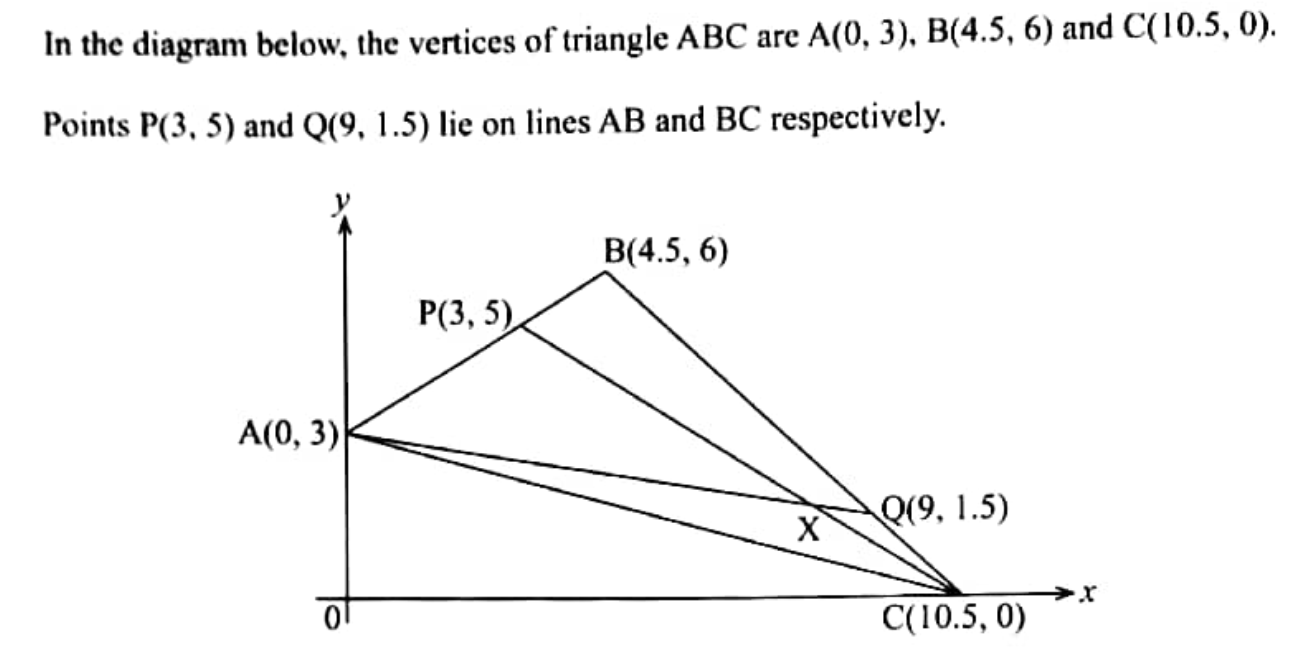
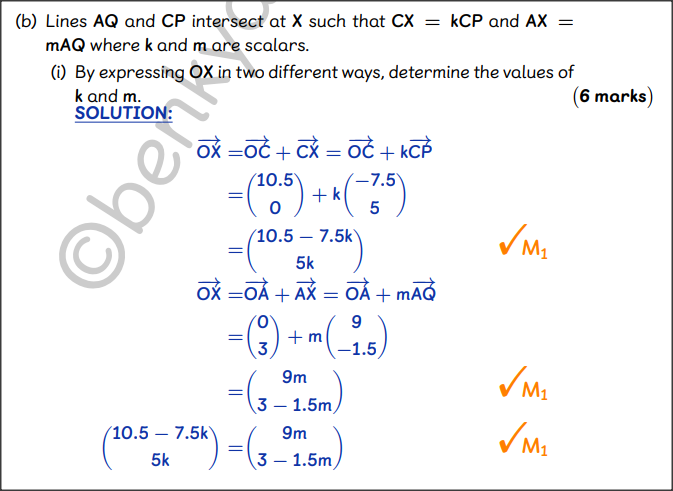
QUESTION 20 | KCSE 2022 | VECTORS I | PAPER 2 | FORM 2 LEVELIn the diagram below, the vertices of triangle ABC are A(0, 3), B(4.5, 6) and C(10.5, 0).
Points P(3, 5) and Q(9, 1.5) lie on lines AB and BC respectively.
QUESTION 19 | KCSE 2022 | MATRICES AND TRANSFORMATION | PAPER 2 | FORM 4 LEVELmaps triangle A'B'C' into triangle A"B"C". The coordinates of point C" is (10, 8) and the area of triangle A"B"C" is 15 square units.
QUESTION 18 | KCSE 2022 | Probability | PAPER 2 | FORM 3 LEVELTwo bags P and Q contain identical marbles except for the colours. Bag P contains 3 green and 4 red marbles. Bag Q contains 2 green and 3 red marbles. (1 mark)
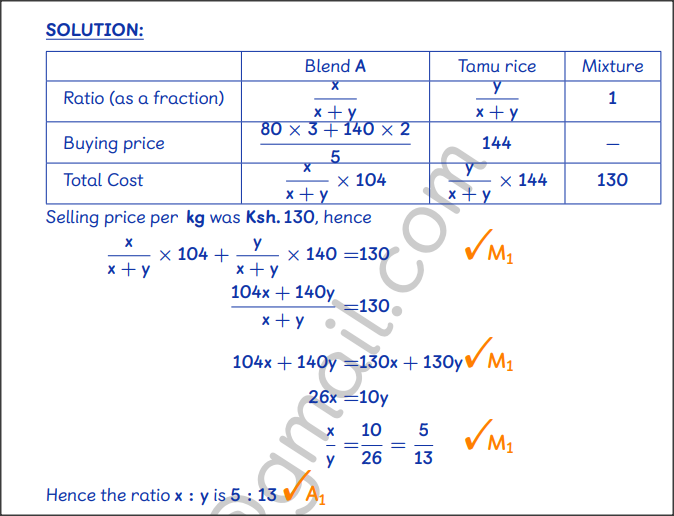
QUESTION 17 | KCSE 2022 | COMPOUND PROPORTIONS AND RATES OF WORK | PAPER 2 | FORM 3 LEVELA wholesaler stocks two types of rice: Refu and Tamu. The wholesale prices of 1 kg of Refu and 1 kg of Tamu are Ksh 80 and Ksh 140 respectively. The wholesaler also stocks blend A rice which is a mixture of Refu and Tamu rice mixed in the ratio 3: 2.
QUESTION 16 | KCSE 2022 | LINEAR MOTION | PAPER 2 | FORM 2 LEVELThe velocity v m/s of a particle moving in a straight line is (-2t+4) m/s. Determine the distance moved by the particle during the first second of its motion. (3 marks)
QUESTION 15 | KCSE 2022 | LONGITUDES | PAPER 2 | FORM 4 LEVELAn aircraft took off from an airport A(0°, 40°W) at 1100 h local time. The aircraft landed at airport B(0°, 65°W) at 1200 h local time.
Determine the speed of the aircraft in knots. (4 marks) QUESTION 14 | KCSE 2022 | VECTORS II | PAPER 2 | FORM 3 LEVELPoint P(8, 4, -1) divides line AB internally in the ratio 4: 1. The position vector of point A with respect to the origin O is [-4 8 3]
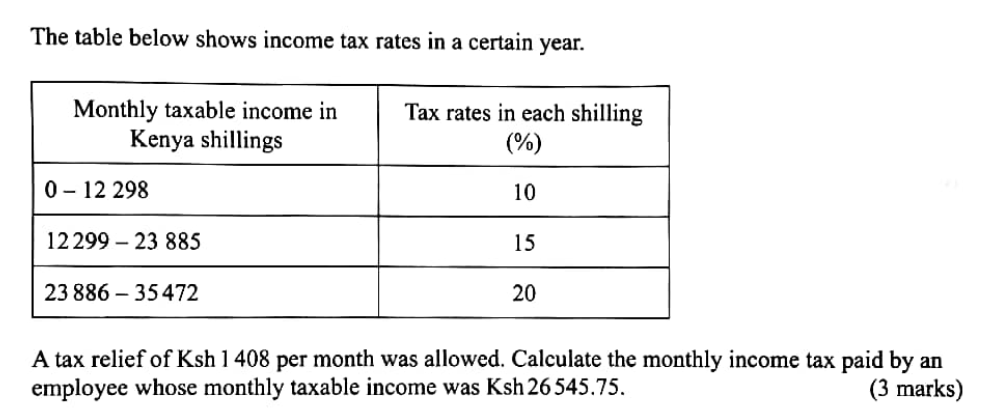
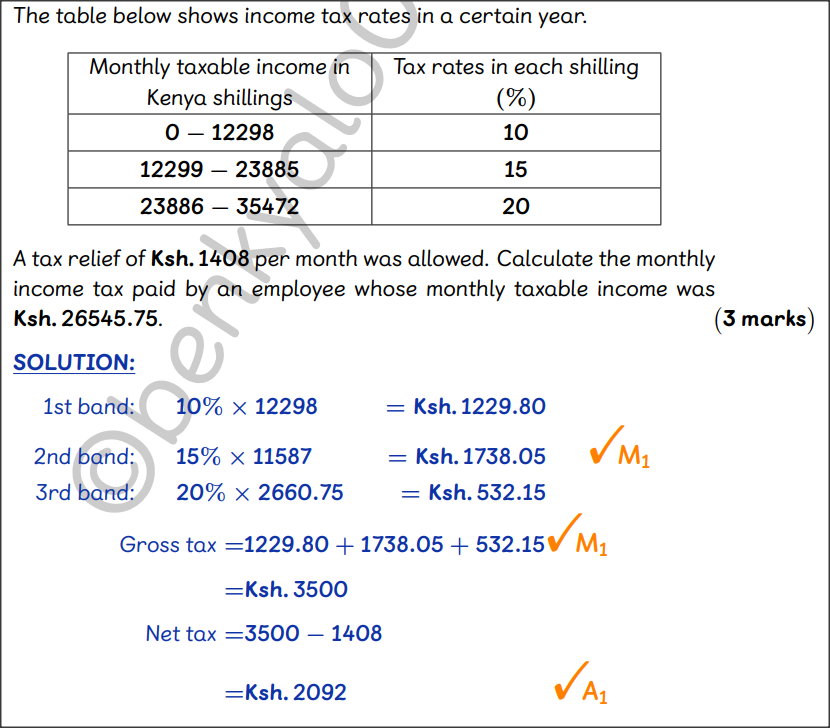
Determine the coordinates of point B. (3 marks) QUESTION 13 | KCSE 2022 | COMMERCIAL ARITHMETICS II | PAPER 2 | FORM 3 LEVEL The table below shows income tax rates in a certain year.
A tax relief of Ksh 1 408 per month was allowed. Calculate the monthly income tax paid by an employee whose monthly taxable income was Ksh 26545.75. (3 marks) QUESTION 12 | KCSE 2022 | STATISTICS II | PAPER 2 | FORM 4 LEVELThe data below represents the number of animals owned by 7 neighbours:
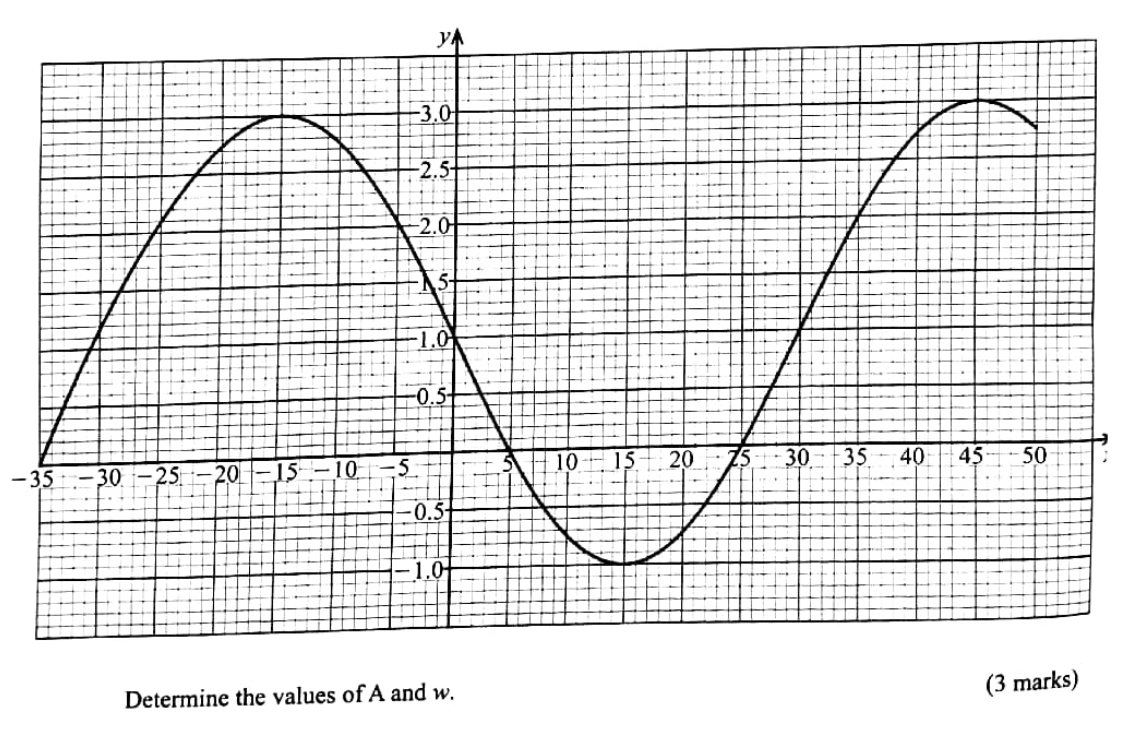
9, 5, 14, 6, 8, 13 and 15. Calculate, correct to the nearest whole number, the standard deviation of the number of animals. (3 marks) QUESTION 11 | KCSE 2022 | TRIGONOMETRY III | PAPER 2 | FORM 4 LEVEL The figure below represents the curve of the function y = 1 − A sin wx for the range −35◦ ≤ x ≤ 50◦. Determine the values of A and R.
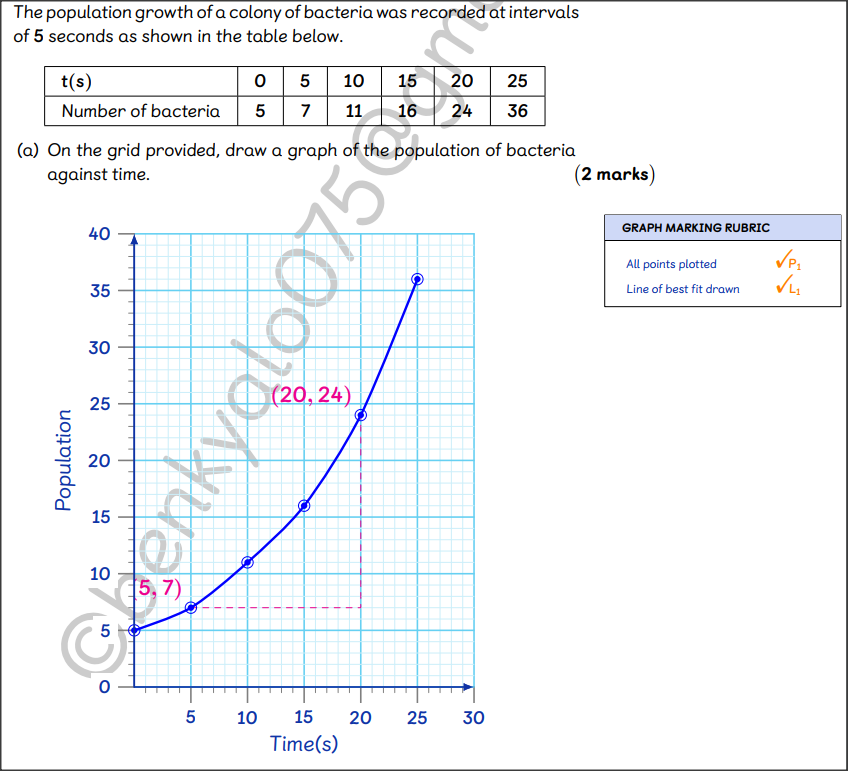
QUESTION 9 | KCSE 2022 | GRAPHICAL METHODS | PAPER 2 | FORM 3 LEVELThe population growth of a colony of bacteria was recorded at intervals of 5 seconds(s) as shown in the table below (a) On the grid provided, draw a graph of the population of bacteria against time. (2 marks) (b) Use the graph to determine, correct to 2 decimal places, the average rate of change of the population of bacteria between t = 5 seconds and t = 20 seconds. (2 marks)
QUESTION 10 | KCSE 2022 | GRAPHICAL METHODS | PAPER 2 | FORM 3 LEVEL A circle centre C(5, 5) passes through points A(1, 3) and B(a, 9). Find the equation of the circle and hence the possible values of a. (3 marks)
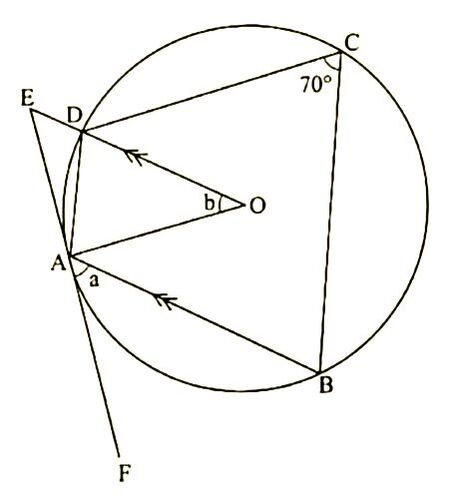
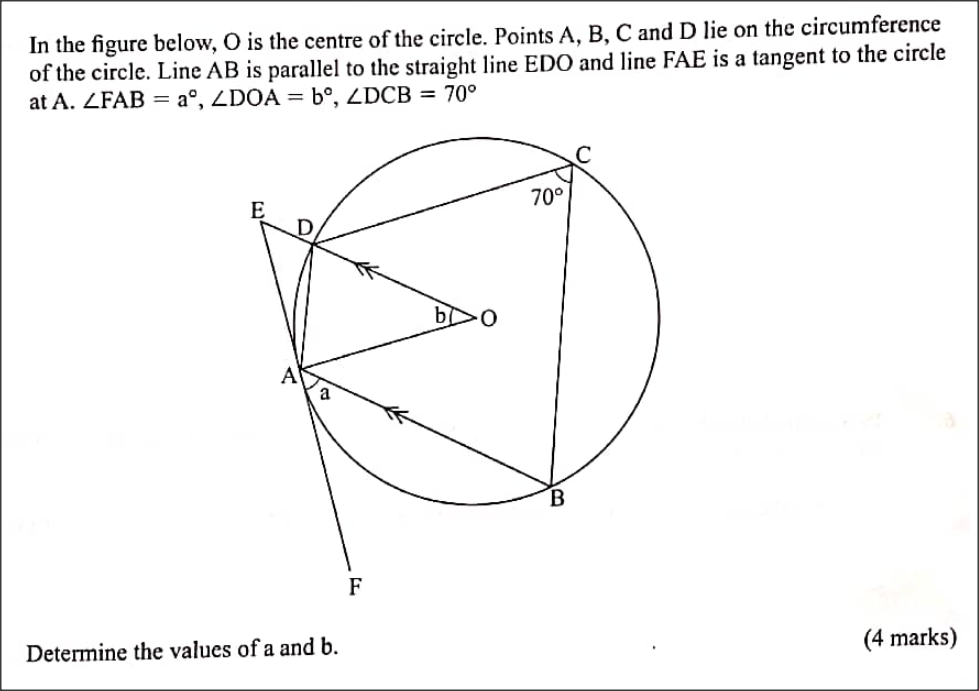
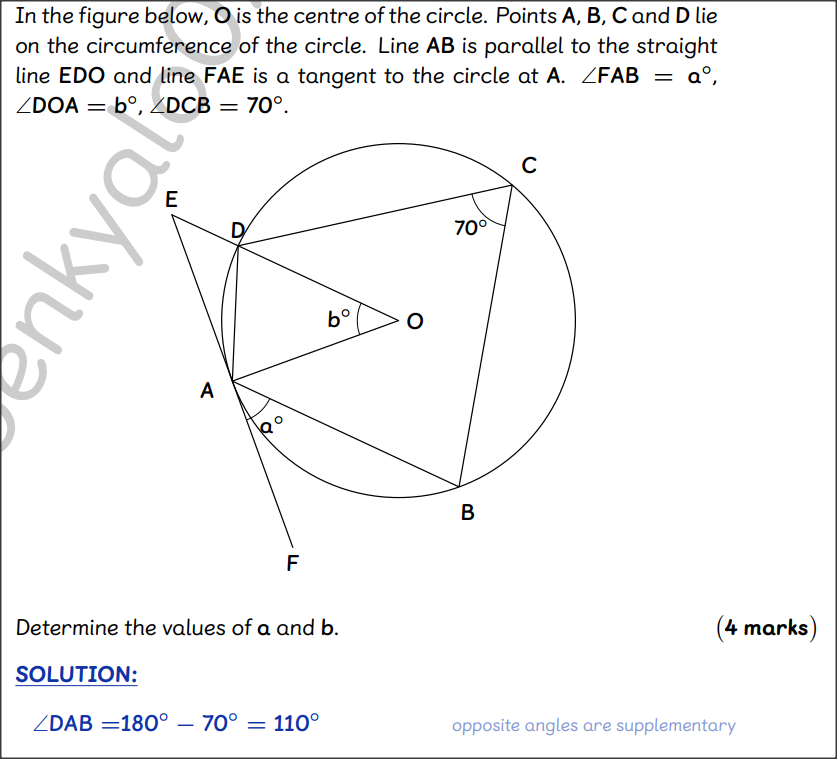
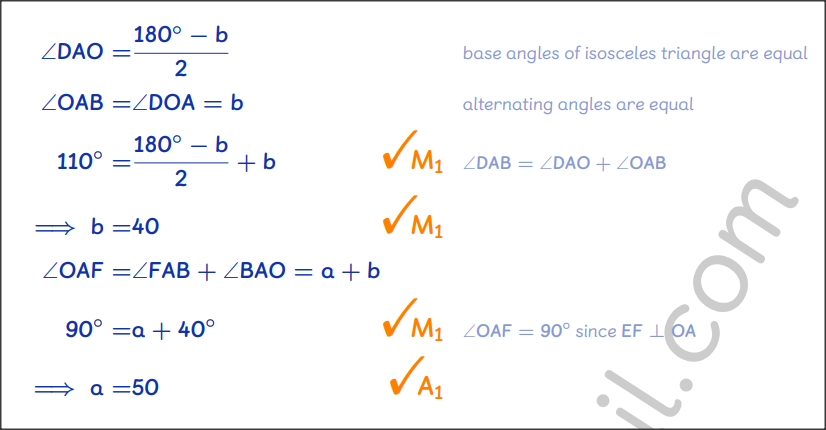
QUESTION 8 | KCSE 2022 | ANGLE PROPERTIES OF A CIRCLE | PAPER 2 | FORM 3 LEVEL In the figure below, O is the centre of the circle. Points A, B, C and D lie on the circumference of the circle. Line AB is parallel to the straight line EDO and line FAE is a tangent to the circle at A. FAB = a°, DOA = b°, DCB = 70°
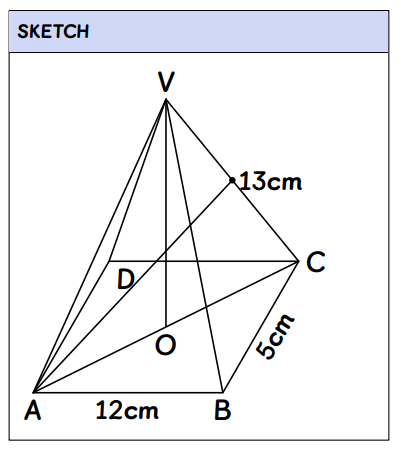
Determine the values of a and b. (4 marks) QUESTION 7 | KCSE 2022 | common solids | PAPER 2 | FORM 1 LEVEL A rectangle ABCD in which AB = 12 cm and BC = 5 cm is the base of a right pyramid whose apex is V. VA = VB = VC = VD = 13 cm. Point M is the mid point of the edge VC. (3 marks)
Calculate, correct to 2 decimal places, the length of line AM. Two parallel chords AB = 4cm and CD = 10 cm lie on opposite sides of a centre O of a circle.19/12/2023 QUESTION 6 | KCSE 2022 | CIRCLES, CHORDS AND TANGENTS | PAPER 2 | FORM 3 LEVEL Two parallel chords AB = 4cm and CD = 10 cm lie on opposite sides of a centre O of a circle. The perpendicular distance between the two chords is 7 cm.
Calculate the radius of the circle leaving the answer in surd form. (3 marks) QUESTION 5 | KCSE 2022 | QUADRATIC EQUATIONS | PAPER 2 | FORM 3 LEVELThe perimeter of a rectangle is 48 cm while it area is 108 cm². Form a quadratic equation to represent the situation and hence determine the dimensions of the rectangle. (3 marks)
QUESTION 4 | KCSE 2022 | FORMULA & VARIATIONS | PAPER 2 | FORM 3 LEVELThe market value of a certain precious stone varies directly as the square of its mass. One such stone of mass 10 kg has a value of Ksh. 600000.
Calculate the value of a similar stone whose mass is 18.5 kg. 3 marks Simplify (3 + √5)/(7 − 3√5), leaving the answer in the form a + b√c where a, b and c are integers.18/12/2023 QUESTION 3 | KCSE 2022 | SURDS | PAPER 2 | FORM 3 LEVELSimplify (3 + √5)/(7 − 3√5), leaving the answer in the form a + b√c where a, b and c are integers.
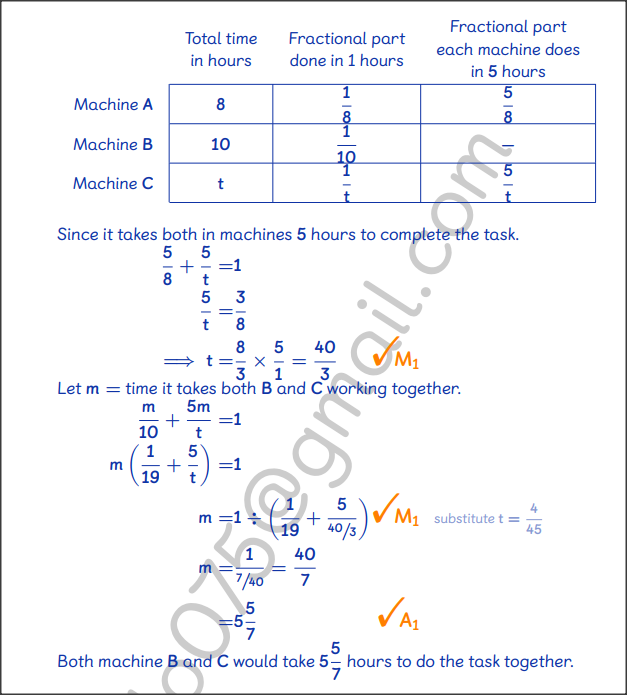
Two machines A and B working independently can take 8 hours and 10 hours respectively to do a task18/12/2023 QUESTION 2 | KCSE 2022 | COMPOUND PROPORTIONS AND RATES OF WORK | PAPER 2 | FORM 3 LEVELTwo machines A and B working independently can take 8 hours and 10 hours respectively to do a task. A third machine C and machine A working together can do the same task in 5 hours. Determine the time it would take machine B and machine C working together to do the same task. 3 marks
QUESTION 1 | KCSE 2022 | SEQUENCES AND SERIES | PAPER 2 | FORM 3 LEVEL An investor took a loan from a bank that charged interest. the loan and the interest accrued were repaid in monthly instalments. The investor repaid Ksh. 1500 in the first month and in each subsequent month the instalments were reducing by Ksh. 50 until the loan was fully repaid. Determine the maximum amount that may be paid for that loan. [3 marks]
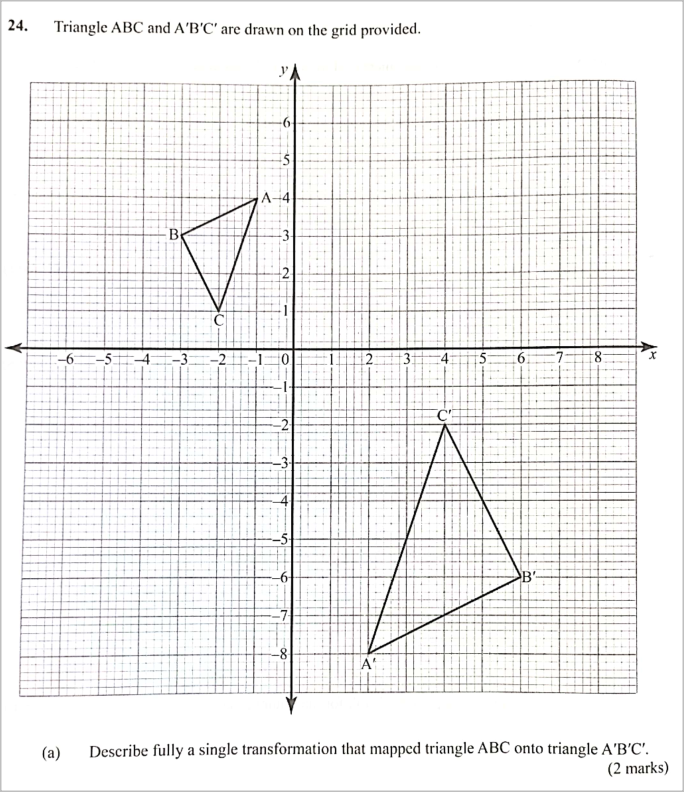
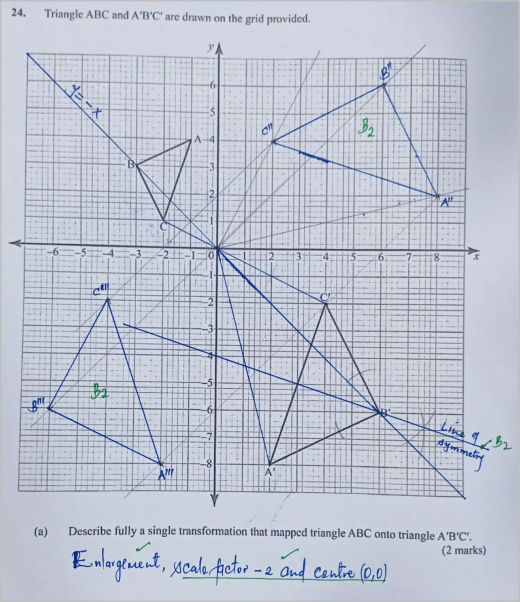
QUESTION 24 | KCSE 2022 | MATRICES AND TRANSFORMATIONS | PAPER 1 | FORM 4 LEVELTriangle ABC and A'B'C' are drawn on the grid provided.
(a) Describe fully a single transformation that mapped triangle ABC onto triangle A'B'C'. (2 marks) (b) On the same grid, draw: (i) triangle A"B"C" the image of triangle A'B'C' under a rotation of +90° about Ο (0, 0). (2 marks) (ii) triangle A"B"C", the image of triangle A"B"C" under a reflection in the line y = -x. (2 marks) (c) Draw the line of symmetry of triangle A'B'C' and hence determine its equation in the form y = mx +c, where m and c are constants. (4 marks) |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|





















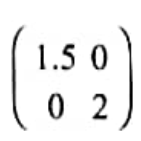
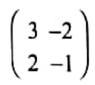









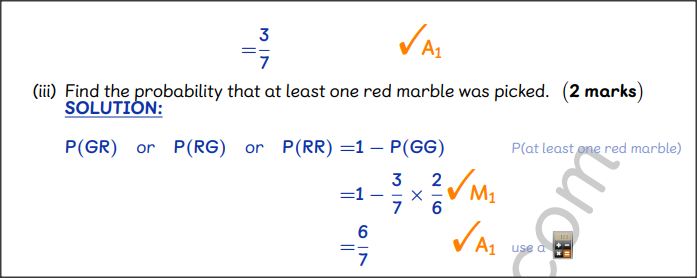



























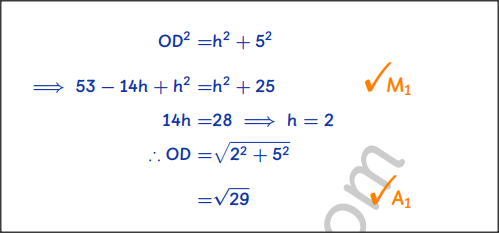


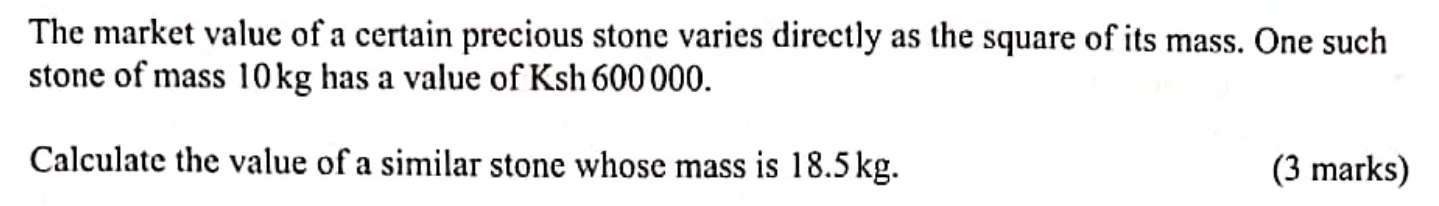


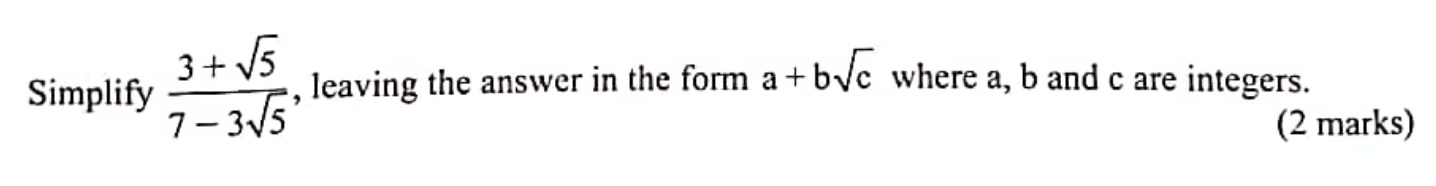








 RSS Feed
RSS Feed