KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
| SIMULTANEOUS EQUATIONS | FORM 3 LEVEL | SECTION I | PAPER 1 | ALT B | KCSE 2011 | QUESTION 15 |Solve the simulataneous equations:
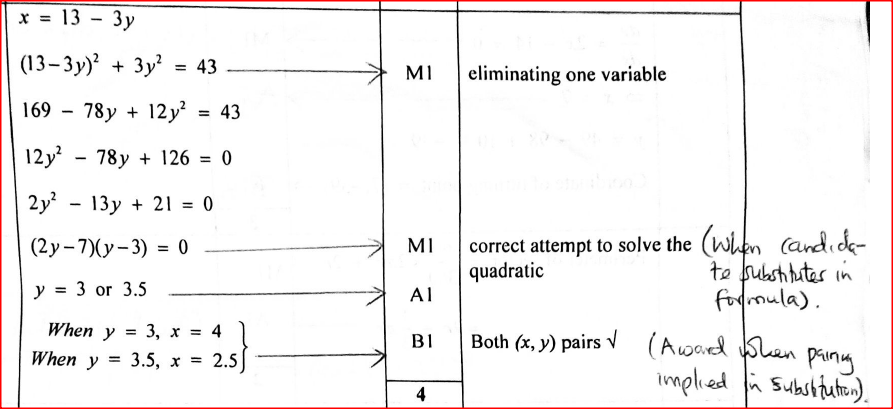
p - q = 3 p² - q² = 21
0 Comments
ALT B | quadratic equations | | FORM 3 LEVEL | SECTION 1 | PAPER 2 | KCSE 2010 | QUESTION 3Solve by factorisation, the quadratic equation:
2x²-3x-50 = 0 (3 marks) ALT B | QUADRATIC EQUATIONS | SECTION 1 | QUESTION 19 | KCSE 2010 | FORM 3 LEVELThe length and width of a rectangular plot of land are given as (7x + 5) m and (x + 10) m respectively.
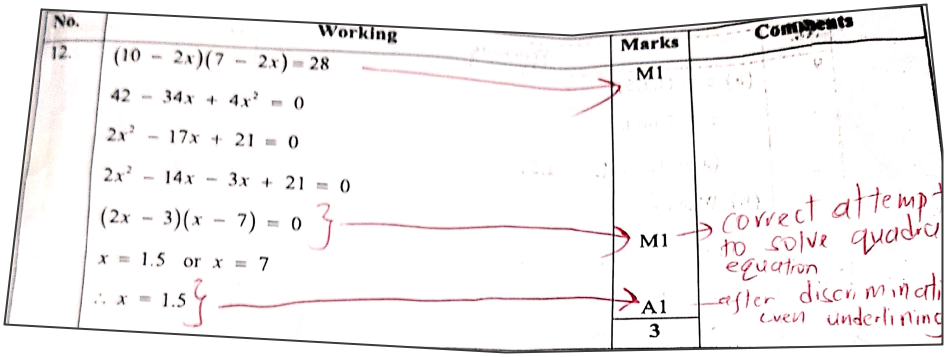
QUESTION 12 | KCSE 2023 | QUADRATIC EQUATIONS | PAPER 2 | FORM 4 LEVELThe length and width of a rectangular floor of a room are 10 m and 7 m respectively. A rectangular carpet of area 28 m² is placed on the floor. The carpet leaves a uniform space of x m with each of the walls of the room.
Form a quadratic equation in x and hence solve for x. (3 marks) QUESTION 7 | KCSE 2023 | Quadratic Expressions | PAPER 1 | FORM 3 LEVELSimplify and hence factorise the expression (5x - 4y) (4x + 5y) - 9xy. (3 marks)
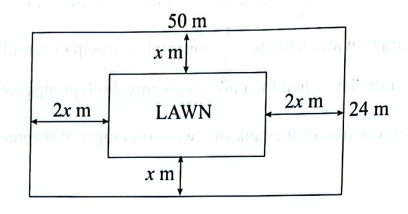
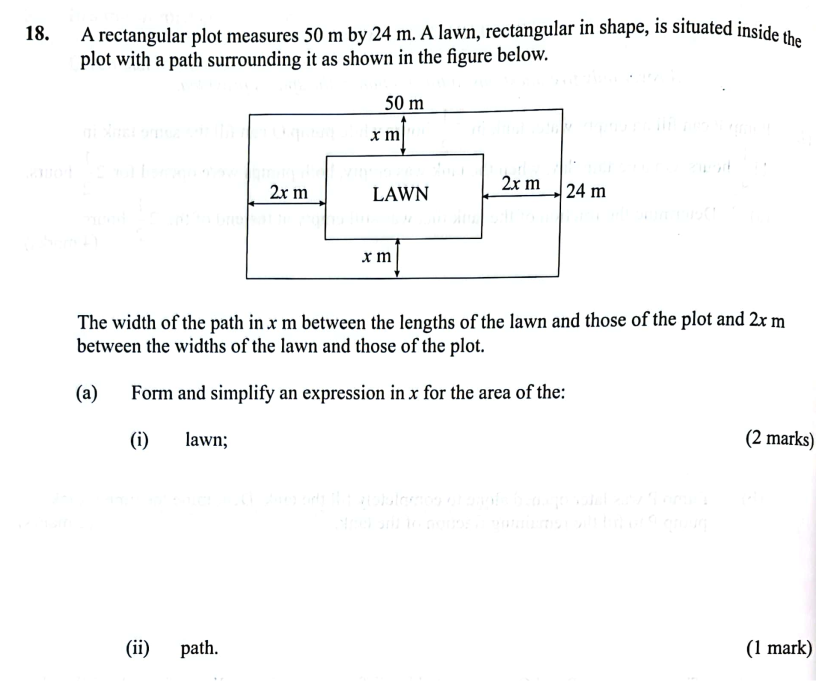
QUESTION 18 | KCSE 2021 | AREA | PAPER 2 | FORM 3 LEVELA rectangular plot measures 50 m by 24 m. A lawn, rectangular in shape, is situated inside the plot with a path surrounding it as shown in the figure below. The width of the path in x m between the lengths of the lawn and those of the plot and 2x m between the widths of the lawn and those of the plot.
QUESTION 3 | KCSE 2021 | Quadratic Equations | PAPER 2 | FORM 3 LEVELThe expression ax² - 30x + 9 is a perfect square, where a is a constant. Find the value of a.
(2 marks) QUESTION 21 | KCSE 2021 | Quadratic Equations | PAPER 1 | FORM 3 LEVEL(a) Solve for x (x - 4)^2 = (x - 8)(2x + 7). (4 marks) (b) John cycled 6 km from his home to school at an average speed of (2x - 3) km/h.
Peter walked 2.4 km from his home to the school at an average speed of x km/h. Peter took 16 minutes less than John. Determine the time, in minutes, that John took to reach the school. (6 marks) QUESTION 7 | KCSE 2021 | Quadratic Expressions | PAPER 1 | FORM 3 LEVELSimplify (4 + 2y)² - (2y - 4)². (2 marks)
K.C.S.E MATHEMATICS Q & A-MODEL 1997PP1QN20(A) Draw The Graph Of Y = 6 + X - X2, Taking Integral Value Of X In -4 ≤ X ≤ 5. (The Grid Is Provided. Using The Same Axes Draw The Graph Of Y = 2 – 2x
(B) From Your Graphs, Find The Values Of X Which Satisfy The Simultaneous Equations Y = 6 + X - X2; Y = 2 – 2x (C) Write Down And Simplify A Quadratic Equation Which Is Satisfied By The Values Of X Where The Two Graphs Intersect. QUESTION 5 | KCSE 2022 | QUADRATIC EQUATIONS | PAPER 2 | FORM 3 LEVELThe perimeter of a rectangle is 48 cm while it area is 108 cm². Form a quadratic equation to represent the situation and hence determine the dimensions of the rectangle. (3 marks)
QUESTION 5 | KCSE 2022 | QUADRATIC EQUATIONS | PAPER 1 | FORM 3 LEVELSimplify: [18ax - (3a-4x)(3a + 4x)] / (3a-8x) (3 marks)QUESTION 1 | KCSE 2022 | QUADRATIC EQUATIONS | PAPER 1 | FORM 3 LEVELSolve for n: 6n/n-a = 25/n
A piece of wire, 18 cm long is cut into two parts. The first part is bent to form the four sides of a rectangle having length x cm and breath 1 cm.
a). State two expressions in terms of x only for the perimeter of the square and the rectangle. (2 marks)
If A =8 cm2, Solve the equation in (b) above for x, hence find the possible dimensions of the two pieces of wire. (6 marks)
Form 3 Mathematics
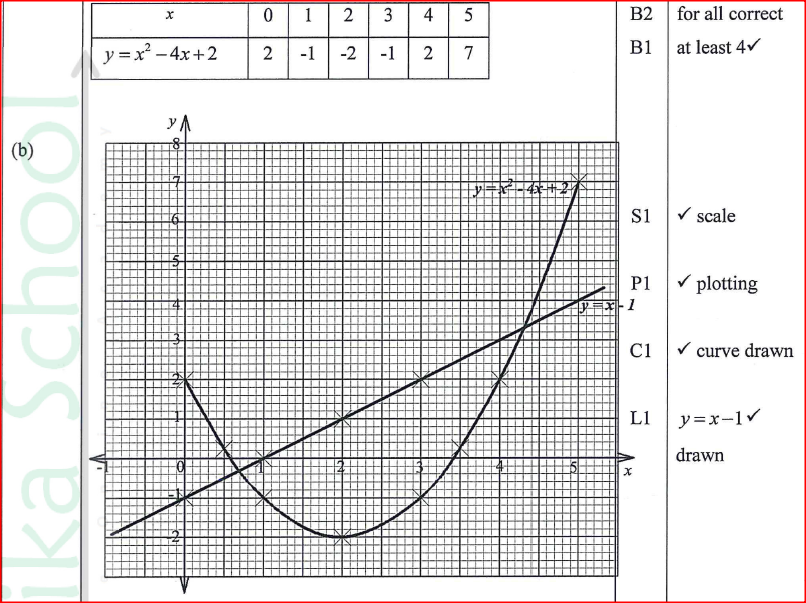
(a)Complete the table below for the equation y = x2-4x+2
(b) On the grid provided draw the graph y = x2 - 4x + 2 for 0 ≤ x ≤ 5. Use 2 cm to represent 1 unit on the x-axis and 1 cm to represent 1 unit on the y-axis.
(c) Use the graph to solve the equation, x2 -4x + 2 = 0 (d) By drawing a suitable line, use the graph in (b) to solve the equation x2 -5x + 3 = 0. |
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|


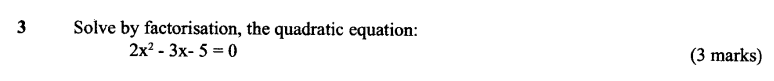





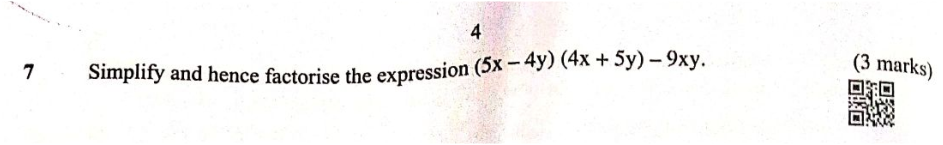










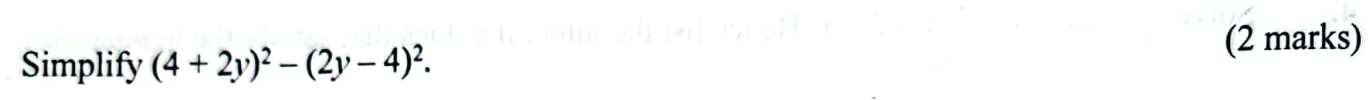








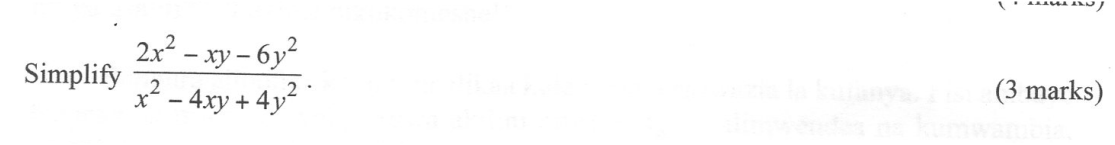

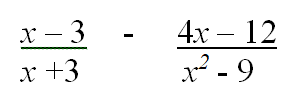
















 RSS Feed
RSS Feed