KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
|
0 Comments
Form 4 Mathematics
The gradient of the curvey y = 2x3 – 9x2 + px – 1 at x = 4 is 36.
a)Find : i) the value of p; ii)The equation of the tangent to the curve at x = 0.5. b) Find the coordinates of the training points of the curve Form 4 Mathematics
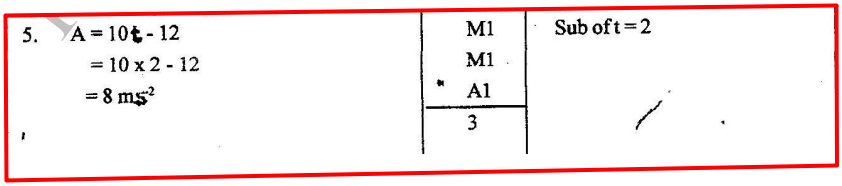
The velocity V ms, of a moving body at time t seconds is given by V = 5t2 – 12t + 7
Find its acceleration after 2 seconds.
Form 4 Mathematics
The gradient of a curve is given by dy/dx = x2 - 4x4- 3. The curve passes through the point (1,0). Find the equation of the curve.
Form 4 Mathematics
Form 4 Mathematics
The equation of acurve is given by y = x3 – 4x2 – 3x
(a) Find the value of y when x = -1 (b) Determine the stationary points of the curve (c) Find the equation of the normal to the curve at x = 1 Form 4 MathematicsThe velocity Vms-1 of particle in motion is given by V =3t2 – t +4, where t is time in seconds. Calculate the distance traveled by the particle between the time t=1 second and t=5 seconds. Form 4 Mathematics
The displacement, s metres, of a moving particle from a point O, after t seconds is given by, s = t3 – 5t2 + 3t + 10
a) Find s when t =2. b) Determine: i. The velocity of the particle when t = 5 seconds; ii. The value of t when the particle is momentarily at rest. c) Find the time, when the velocity of the particles is maximum. Form 4 Mathematics
The acceleration of a body moving along a straight line is (4 - t) m/s2 and its velocity is v m/s after t seconds.
(a) (i) If the initial velocity of the body is 3 m/s, express the velocity v in terms of t. (ii) Find the velocity of the body after 2 seconds. (b) Calculate: (i) the time taken to attain maximum velocity; (ii) the distance covered by the body to attain the maximum velocity. Form 4 Mathematics
The displacement s metre of a particle moving along straight line after t seconds is given by. S = 3t + 3/2 t2 – 2t3
Form 4 Mathematics
The displacement, s metres, of a moving particle after,t seconds is given by, s =2t 3- 5t2 + 4t + 2. .
Determine: (a) the velocity of the particle when t = 3 seconds; (b) the value o f t when the particle is momentarily at rest; (c) the displacement when the particle is momentarily at rest; (d) the acceleration of the particle when t = 3 seconds. Form 2 Mathematics
In a uniformly accelerated motion the distance, s metres, travelled in time t seconds varies partly as the time and partly as the square of the time. When the time is 2 seconds, the distance travelled is 80 metres and when the time is 3 seconds, the distance travelled is 135 metres.
(a) Express s in terms of t. (b) Find: (i) the distance travelled in 5 seconds; (ii) the time taken to travel a distance of 560 metres. Form 4 Mathematics
A particle starts from O and moves in a straight line so that its velocity V ms-1 after time t seconds is given by V = 3t-t2. The distance of the particle from O at time t seconds is s metres.
(a) Express s in terms of t and c where c is a constant. (b) Calculate the time taken before the particle returns to 0. Form 4 MathematicsGiven the curve y = 2x3 + ½x2 – 4x + 1. Find the:
Form 4 Mathematics
A particle moves in a straight line from a fixed point. Its velocity Vms-1 after t seconds is given by V=9t2 – 4t +1
Calculate the distance traveled by the particle during the third second. Form 4 Mathematics
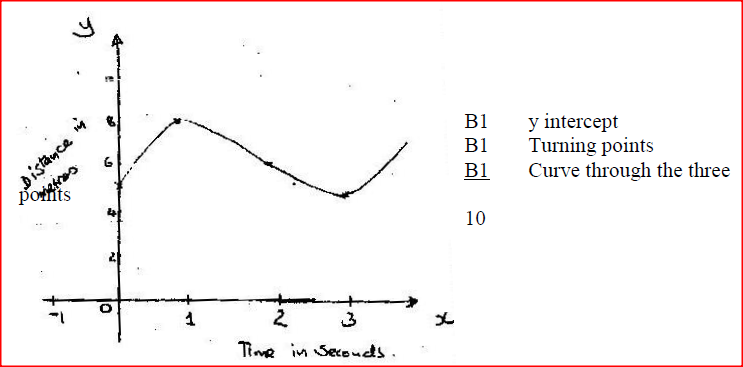
The distance s metres from a fixed point O, covered by a particle after t seconds is given by the equation;
S =t3 -6t2 + 9t + 5. a) Calculate the gradient to the curve at t=0.5 seconds b) Determine the values of s at the maximum and minimum turning points of the curve. c) On the space provided, sketch the curve of s= t3-6t2+9t + 5. Form 4 Mathematics
A particle moves in a straight line through a point P. Its velocity v m/s is given by v= 2 -1, where t is time in seconds, after passing P. The distance s of the particle from P when t = 2 is 5 metres. Find the expression for s in terms of t.
Form 4 Mathematics
The gradient of the tangent to the curve y = ax3 + bx at the point ( 1,1) is -5
Calculate the values of a and b Form 4 MathematicsThe displacement x metres a particle after seconds given by:
x = t3- 2t2 + 6t > 0.
Form 4 MathematicsForm 4 MathematicsForm 4 MathematicsFind the equation of the tangent to the curve Y = (x2 + 1) (x - 2) when x = 2 Free 1999 K.C.S.E Mathematics Topical Question & Answers Paper 1
A particle moves on a straight line. The velocity after t seconds is given by V = 3t2 – 6 t – 8. The distance of the particle from the origin after one second is 10 metres. Calculate the distance of the particle from the origin after 2 seconds.
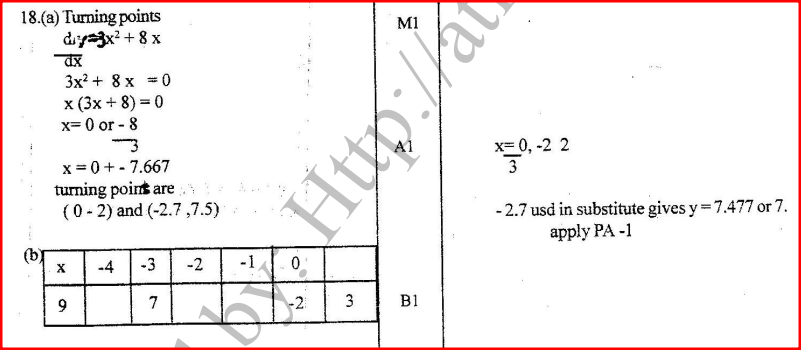
The curve y = ax3 — 3x2 — 2x + 1 has the gradient 7 when x=l. Find the value of aThe equation of a curve is y = 3x2 - 4 x + 1
|
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|
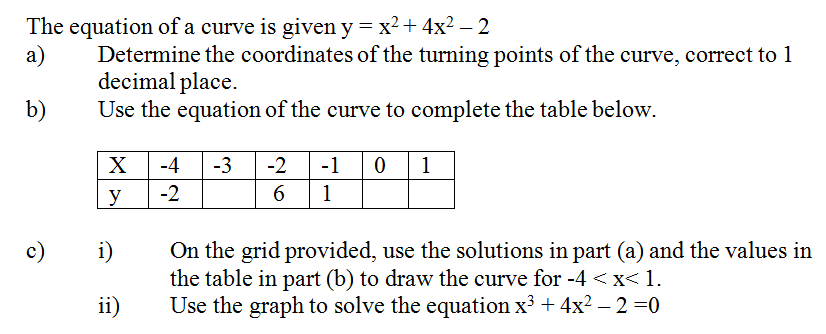


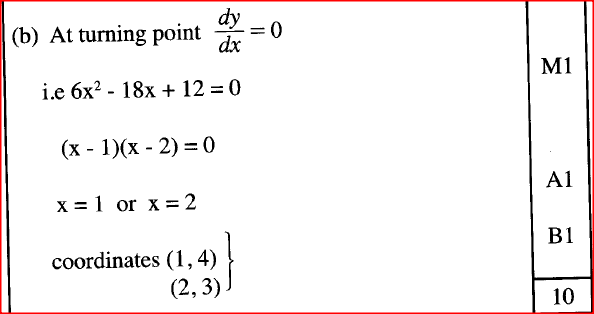
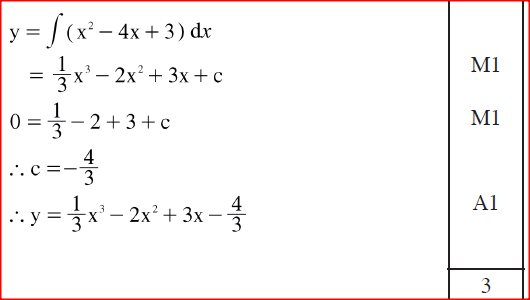






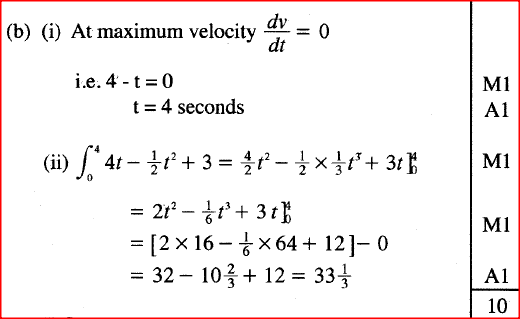

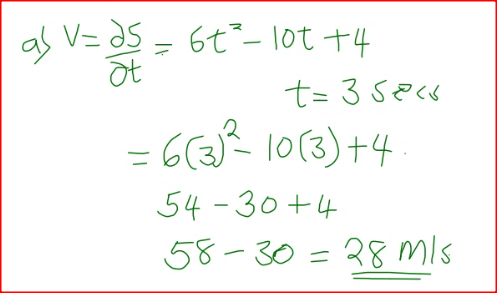
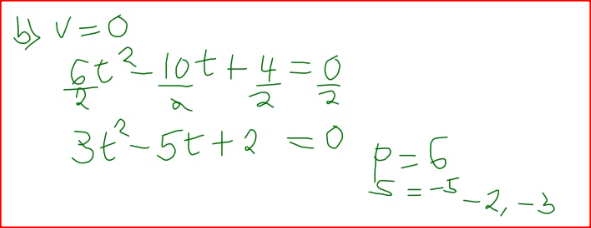
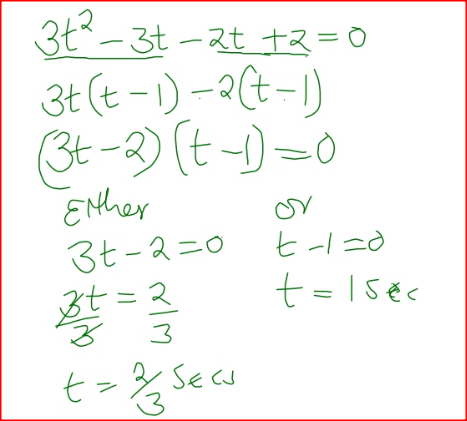
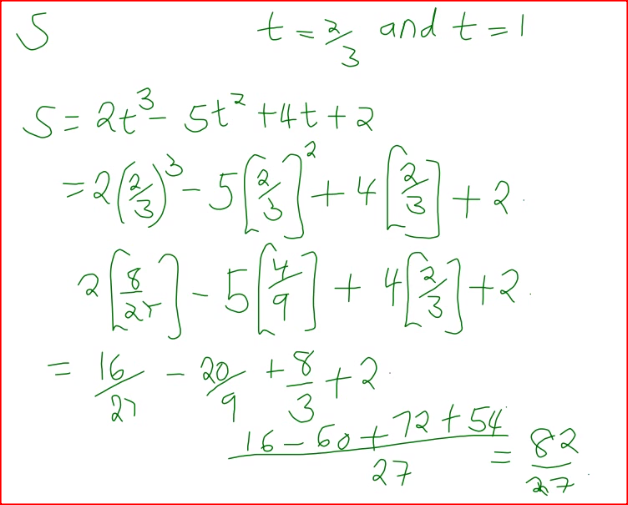
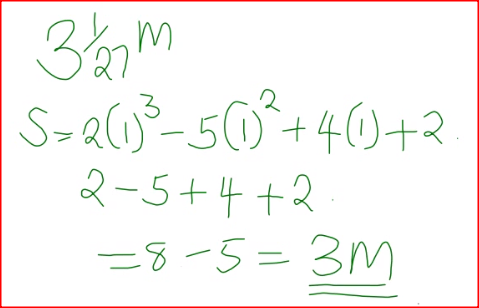
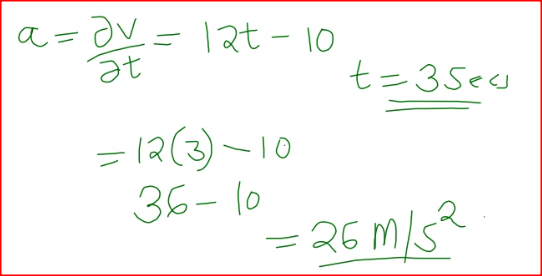


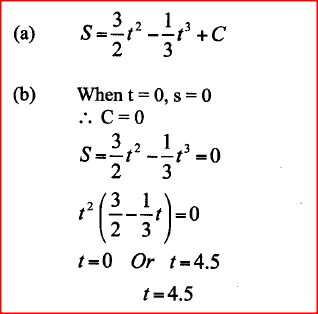


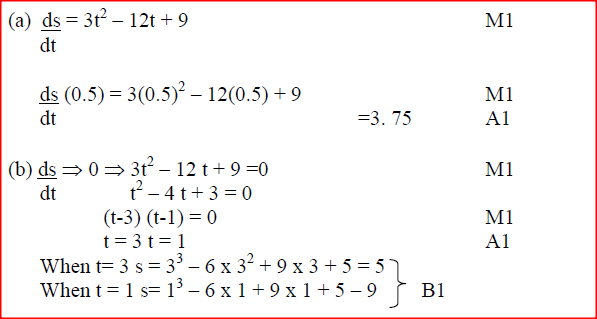



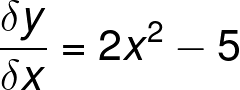








 RSS Feed
RSS Feed