KCSE MATHEMATICS QUESTIONS AND SOLUTIONS ~ Topically Analyzed
Form 4 Mathematics
The displacement, s metres, of a moving particle after,t seconds is given by, s =2t 3- 5t2 + 4t + 2. .
Determine: (a) the velocity of the particle when t = 3 seconds; (b) the value o f t when the particle is momentarily at rest; (c) the displacement when the particle is momentarily at rest; (d) the acceleration of the particle when t = 3 seconds.
0 Comments
Form 4 Mathematics
(a) Using the trapezium rule with seven ordinates, estimate the area of the region bounded by the curve y = -x2 +,6x+ 1, the lines x = 0, y = 0 and x = 6.
(b) Calculate: (i) the area of the region in (a) above by integration; (iii) the percentage error of the estimated area to the actual area of the region,correct to two decimal places. Form 2 Mathematics
In a triangle ABC, BC =8 cm, AC= 12 cm and angle ABC = 120°.
(a) Calculate the length of AB, correct to one decimal place. (b) If BC is the base of the triangle, calculate, correct to one decimal place: (i) the perpendicular height of the triangle; (ii) the area of the triangle; (iii) the size of angle ACB. Form 4 Mathematics
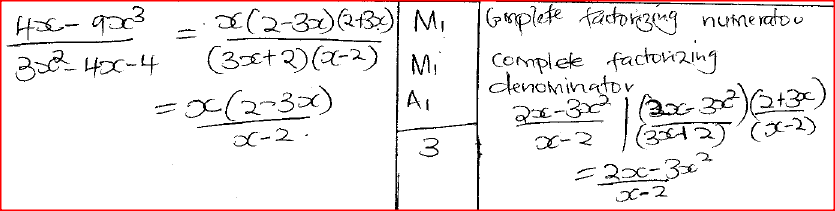
Find the value of p.
(b) A saleswoman earned a fixed salary of Ksh x and a commission of Ksh y for each item sold. In a certain month she sold 30 items and earned a total of Ksh 50 000. The following month she sold 40 items and earned a total of Ksh 56 000. (i) Form two equations in x and y. (ii) Solve the equations in (i) above using matrix method. (iii) In the third month she earned Ksh 68 000. Find the number of items sold. Form 2 Mathematics
Makau made a journey of 700 km partly by train and partly by bus. He started his journey at 8.00 a.m. by train which travelled at 50 km/h. After alighting from the
train, he took a lunch break of 30 minutes. He then continued his journey by bus which travelled at 75 km/h. The whole journey took 11 1/2 hours. (a) Determine: (i) the distance travelled by bus; (ii) the time Makau started travelling by bus. (b) The bus developed a puncture after travelling 187 1/2 km. It took 15 minutes to replace the wheel. Find the time taken to complete the remaining part of the journey Form 2 Mathematics
A solid consists of a cone and a hemisphere. The common diameter of the cone and the hemisphere is 12 cm and the slanting height of the cone is 10 cm.
(a) Calculate correct to two decimal places: (i) the surface area of the solid; (ii) the volume of the solid (b) If the density of the material used to make the solid is 1.3 g/cm3, calculate its mass in kilograms. Form 2 Mathematics
A small cone of height 8 cm is cut off from a bigger cone to leave a frustum of height 16 cm, if the volume of the smaller cone is 160 cm3, find the
volume of the frustum Form 1 Mathematics
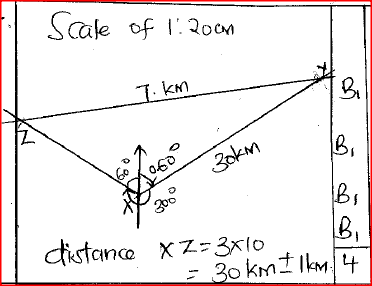
Three police posts X, Y and Z are such that Y is 50 km on a bearing of 060° from X while Z is 70 km from Y and on a bearing of 300° from X.
(a) Using a suitable scale, draw a diagram to represent the above situation. (b) Determine the distance, in km, of Z from X. Form 1 Mathematics
(a) Express 10500 in terms of its prime factors.
(b) Determine the smallest positive number P such that 10500P is a perfect cube. Form 1 Mathematics
In January, Mambo donated 1/6th of his salary to a children's home while Simba donated 1/5th of his salary to the same children's home. Their total donation for
January was Ksh. 14 820. In February, Mambo donated 1/8th of his salary to the children's home while Simba donated 1/12th of his salary to the children's home. Their total donation for February was Ksh 8 675. Calculate Mambo 's monthly salary. Form 2 Mathematics
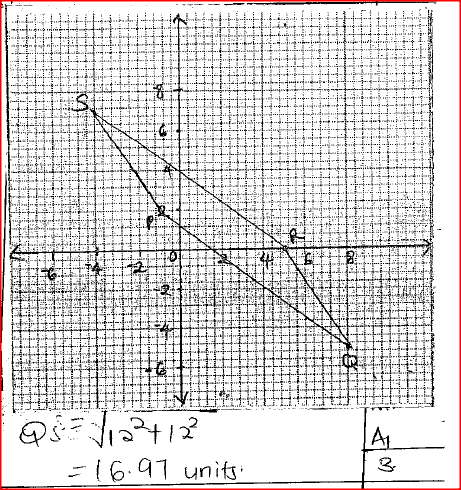
Three vertices of a parallelogram PQRS are P(-l, 2), Q(8, -5) and R (5,0).
(a) On the grid provided below draw the parallegram PQRS. (b) Determine the length of the diagonal QS. Form 1 Mathematics
A customer paid Ksh. 5 880 for a suit after she was allowed a discount of 2% on the selling price. If the discount had not been allowed, the shopkeeper would have
made a profit of 20% on the sale of the suit. Calculate the price at which the shopkeeper bought the suit. Form 2 MathematicsForm 1 Mathematics
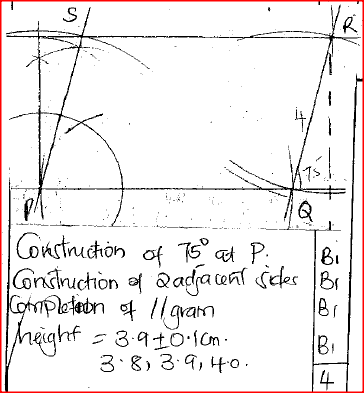
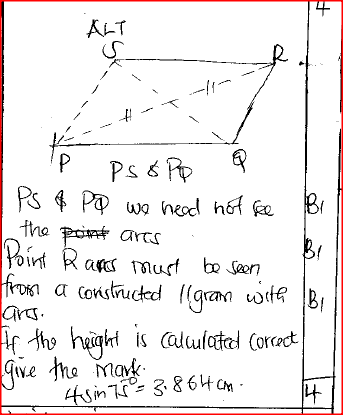
Using a ruler and a pair of compases only:
(a) construct a parallelogram PQRS in which PQ = 6 cm, QR = 4 cm and angle SPQ= 75°; (b) determine the perpendicular distance between PQ and SR. Form 2 Mathematics
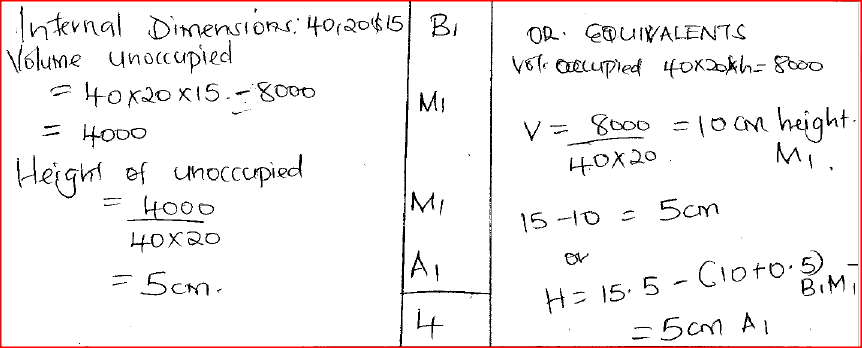
The external length, width and height of an open rectangular container are 41 cm, 21 cm and 15.5 cm respectively. The thickness of the material making the container is 5 mm. If the container has 8 litres of water, calculate the
internal height above the water level. Form 3 Mathematics
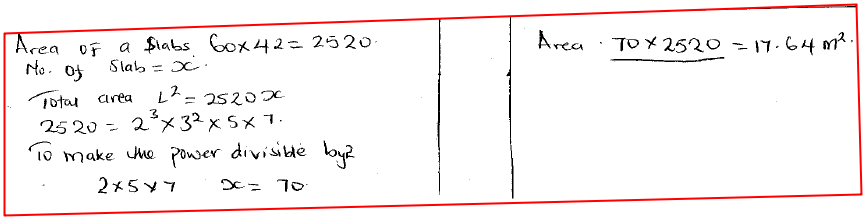
A square room is covered by a number of whole rectangular slabs of sides 60cm by 42 cm. Calculate the least possible area of the room in square rnetres.
Form 2 Mathematics
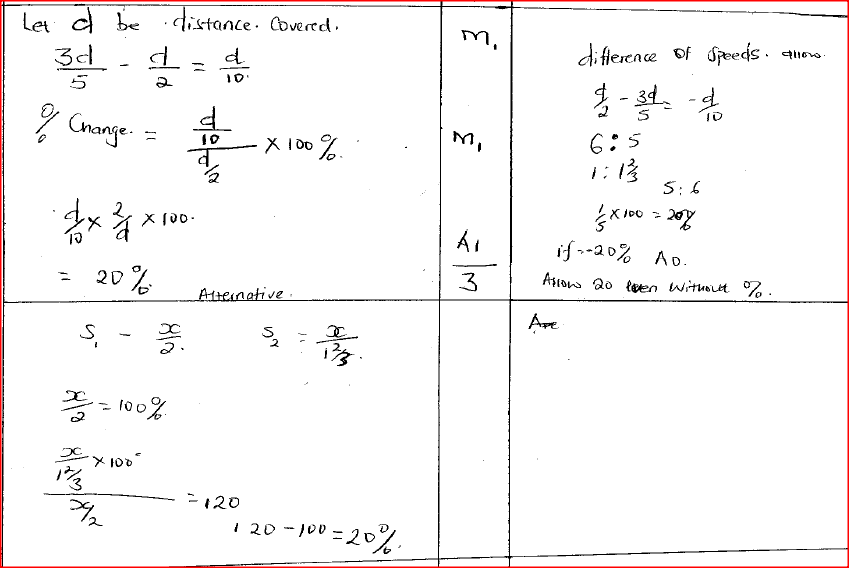
A motorist took 2 hours to travel from one town to another town and 1 hour 40 minutes to travel back. Calculate the percentage change in the speed of the motorist.
Form 1 Mathematics
The diagonal of a rectangular garden measures 11 1/4 m while its width measures 6 3/4 m.Calculate the perimeter of the garden.
|
Categories
All
Archives
December 2024
Latest Posts |
We Would Love to Have You Visit Soon! |
Hours24 HR Service
|
Telephone0728 450425
|
|
8-4-4 materialsLevels
Subjects
|
cbc materialsE.C.D.E
Lower Primary
Upper Primary
Lower Secondary
Upper Secondary
|
teacher support
Other Blogs
|
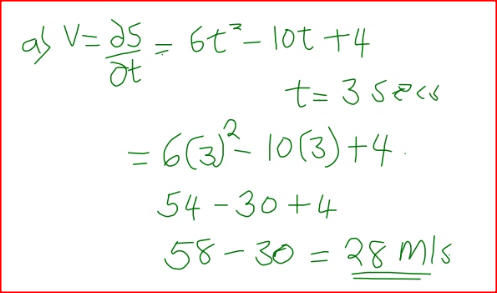
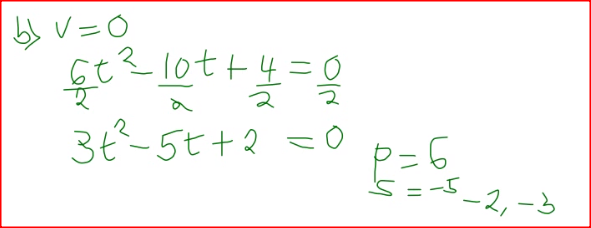
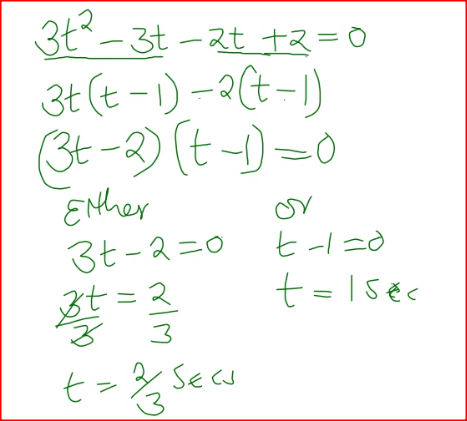
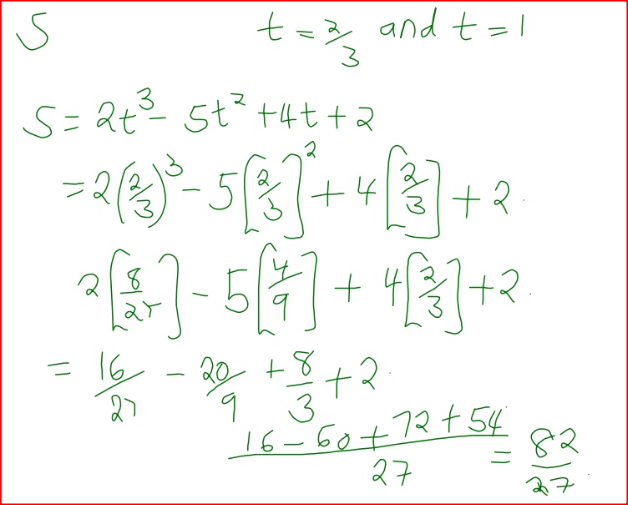
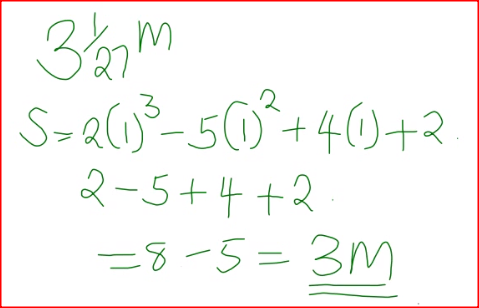
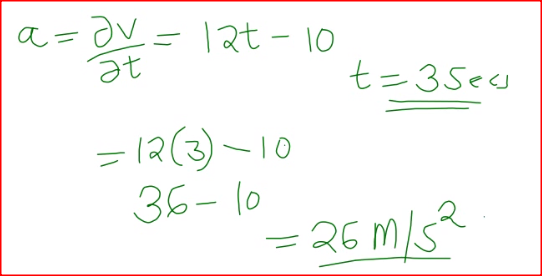

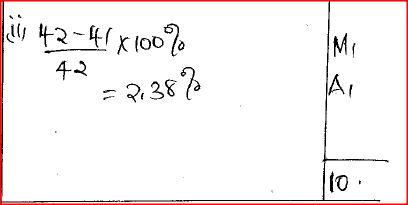
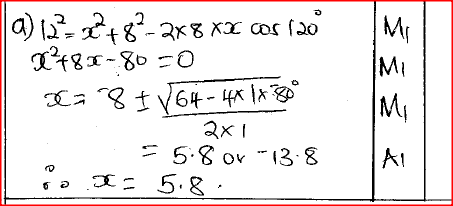
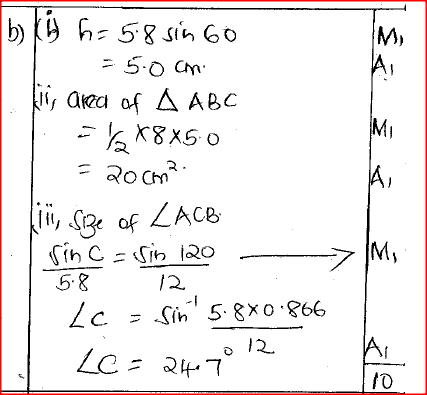
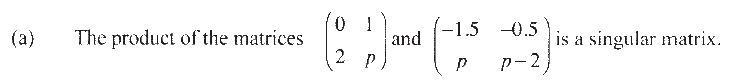
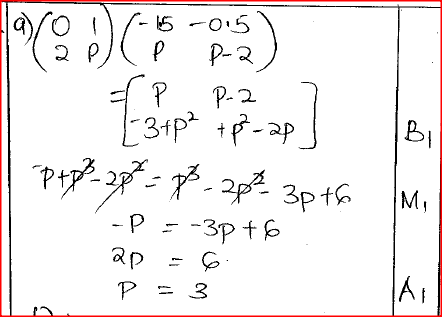





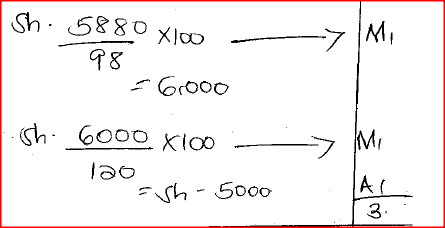

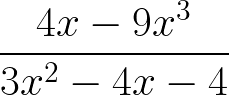
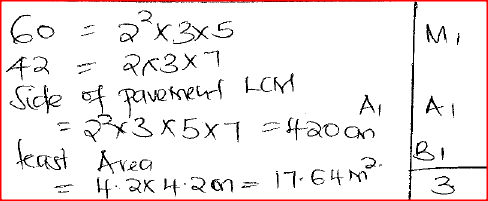

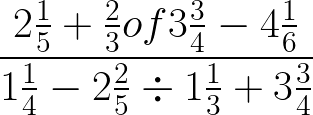


 RSS Feed
RSS Feed